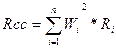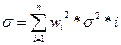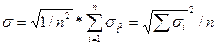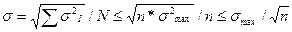Риск и доходность портфельных инвестиций
Существуют различные определения понятия «риск». Так, в наиболее общем виде под риском понимают вероятность возникновения убытков или недополучения доходов по сравнению с прогнозируемым вариантом. В приложении к финансовым активам используют следующую интерпретацию риска и его меры: рисковость актива характеризуется степенью вариабельности дохода, который может быть получен благодаря владению данным активом. Так, государственные ценные бумаги обладают небольшим риском, поскольку вариация дохода по ним в стабильной, не подверженной кризисом экономике практически равна нулю. Напротив, обыкновенная акция любой компании представляет собой значительно более рисковый актив, поскольку доход по таким акциям может ощутимо варьировать. Активы, с которыми ассоциируется относительно больший размер возможных потерь, рассматриваются как более рисковые; вполне естественно, что к таким активам предъявляются и большие требования в отношении доходности. Количественно риск может быть охарактеризован как некий показатель, измеряющий вариабельность дохода. Для этой цели можно использовать размах вариации, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Рассмотрим акции двух компаний А и Б. Пусть в следующем году могут случиться такие события:
Рассчитаем среднюю ставку доходности для каждой компании по формуле:
Средняя ставка доходности составит: Для компании А: R срА = 0,3*0,8+0,5*0,16+0,2*(-0,6) = 0,2=20% Для компании Б: R срБ =0,3*0,25+0,5*0,15+0,2*0,1=0,17=17% Найдем степень разбросанности доходов каждой компании около среднего значения Rср. Для этого вычислим среднее квадратическое отклонение по формуле:
Заполним таблицу:
Итак, для компании А среднее квадратическое отклонение σ А=48,6, для компании Б - σ Б -5,57. Акции компании А более рискованные, так как σ А > σ Б. Рассчитаем для каждой компании коэффициент вариации: Сv = σ / Rср Для компании А – Сv=48.66/20=2.433 Для компании Б Сv=5,57/17=0,328
Сva /Cvб=2,433/0,328=7,42.
Акции компании А в 7,42 раза рискованнее акций компании Б. Пусть имеется портфель облигаций, каждая бумага имеет в портфеле свой вес W i и свою ставку дохода Ri. Оценим ожидаемую ставку доходности как средневзвешенную всех ставок доходности бумаг, имеющихся в портфеле:
Рассмотрим портфель, который состоит из четырех видов ценных бумаг, равных по занимаемому объему, и ставки доходности для них следующие, %: 14; 35; 20; 18. Тогда ожидаемая доходность портфеля— Rср = 21,75%. Предположим, что бумаги не скоррелированы (слабо зависят друг от друга, т. е. коэффициент корреляции стремится к нулю). Найдем дисперсию для всего портфеля:
Мера риска по всему портфелю: _________________ σ = √∑ wi 2 * σ I 2
Рассмотрим частный случай, когда бумаги в портфеле занимают одинаковый объем. В этом случае вес одной бумаги в портфеле — wi =1/n, следовательно:
Выберем из всех σi, максимальное, тогда среднее квадратическое отклонение дохода по всему портфелю:
т. е. получим формулу для оценки рискованности портфеля. Если количество бумаг достаточно велико, то рискованность портфеля стремится к нулю. Вывод: чем больше ценных бумаг в портфеле большого числа эмитентов, тем меньшей рискованностью обладает портфель.
|

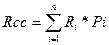
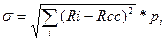
 Составим отношение:
Составим отношение: