Центральная предельная теорема
Вторая группа предельных теорем исследует предельные законы распределения случайной величины. Эта группа теорем носит название «центральной предельной теоремы». Различные её формы посвящены установлению условий, при которых возникает нормальный закон распределения. Иногда эту теорему называют законом ошибок, так как именно в теории ошибок измерений нормальный закон впервые был обоснован П.С. Лапласом и К.Ф. Гауссом. Ошибки физических измерений, астрономических наблюдений, ошибки измерений в биологии, демографии, как правило, распределяются нормально. Дело в том, что такие ошибки являются обычно суммой большого числа мелких ошибок, каждая из которых, взятая в отдельности, не оказывает решающего влияния на суммарную ошибку. Именно такая ситуация рассматривается в центральной предельной теореме, доказанной А.М. Ляпуновым. Теорема Ляпунова. Если
то закон распределения суммы Условие (5.16) обеспечивает ничтожное влияние каждой из случайных величин на его сумму. Теорему принимаем без доказательства. Неограниченное приближение закона распределения суммы
где В качестве следствия из этой теоремы можно получить теорему Муавра –Лапласа о сходимости биноминального распределения к нормальному. Теорема Муавра – Лапласа. Пусть
Вероятность попадания Y в интервал
Значения a и
Итак, если проводится n независимых опытов, в каждом из которых событие A может появиться с вероятностью p, то для любого интервала
Пример 2. Завод выпускает 90 % изделий первого сорта и Р е ш е н и е. Вероятность выбора изделия первого сорта p = 0,3, число опытов n= 1000. Следовательно, np = 900, npq = 90. Применяя формулу (5.21), получим
Пример 3. Для космического корабля вероятность столкновения в течение часа с метеоритом равна 0,001. Найти практически достоверные границы числа столкновений с метеоритом в течение трех месяцев – с 1 июля по 31 августа, если вероятность практической достоверности принимается равной 0,9995. Р е ш е н и е. Количество опытов n = 24∙92 = 2 206 (часов), в течение каждого часа вероятность столкновения p= 0,001 => q = = 1 –p = 0,999. Число столкновений Y – величина, распределенная нормально с
откуда Следовательно, число столкновений
Таким образом, число столкновений космического корабля с метеоритом в течение трех месяцев составляет до 7 раз. Контрольные вопросы 1. В чем заключается сущность закона больших чисел? 2. Как записывается неравенство Чебышева? 3. Какое практическое и теоретическое значение имеет правило Чебышева? 4. Сформулируйте и докажите теорему Чебышева. 5. Сформулируйте и докажите обобщенную теорему Чебышева. 6. Какое практическое значение имеют теоремы Чебышева? 7. Сформулируйте и докажите теорему Бернулли. 8. Как формулируется теорема Пуассона? 9. В чем заключается сущность центральной предельной теоремы? 10. Сформулируйте и докажите теорему Ляпунова. 11. Сформулируйте теорему Муавра – Лапласа. 12. Приведите примеры задач, при решении которых применяется теорема Муавра – Лапласа.
|

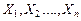 независимые случайные величины, у каждой из которых существует математическое ожидание
независимые случайные величины, у каждой из которых существует математическое ожидание 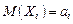 ; дисперсия
; дисперсия  ; абсолютный центральный момент третьего порядка
; абсолютный центральный момент третьего порядка 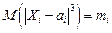 и
и , (5.16)
, (5.16) при
при 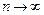 неограниченно приближается к нормальному с математическим ожиданием
неограниченно приближается к нормальному с математическим ожиданием  и дисперсией
и дисперсией  .
.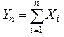 к нормальному закону при
к нормальному закону при  ( 5.17)
( 5.17) – функция Лапласа ( 2.39 ).
– функция Лапласа ( 2.39 ). случайные величины, фигурирующие в теореме Ляпунова, одинаково распределены, дискретны и принимают только два возможных значения 1 и 0 с вероятностями p и q= 1– p. Как и в теореме Бернулли, будем считать, что Xi – это число появлений события A в i- мопыте
случайные величины, фигурирующие в теореме Ляпунова, одинаково распределены, дискретны и принимают только два возможных значения 1 и 0 с вероятностями p и q= 1– p. Как и в теореме Бернулли, будем считать, что Xi – это число появлений события A в i- мопыте  . Тогда число появлений события A в n опытах равно
. Тогда число появлений события A в n опытах равно  . По теореме Ляпунова закон распределения Y при
. По теореме Ляпунова закон распределения Y при  .
.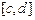 выражается через функцию Лапласа
выражается через функцию Лапласа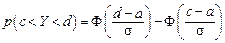 . (5.18)
. (5.18) легко вычисляются;
легко вычисляются;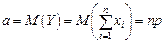 ; (5.19)
; (5.19)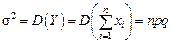 . (5.20)
. (5.20) справедливо соотношение:
справедливо соотношение: . (5.21)
. (5.21)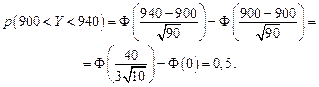
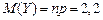 и
и 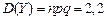 . По теореме Муавра – Лапласа:
. По теореме Муавра – Лапласа: ,
, .
. , т.е.
, т.е.  .
.


