Распределение Хи-квадрат, Стьюдента, Фишера
1. Распределение Хи-квадрат Дифференциальная функция этого распределения имеет вид:
где С увеличением числа степеней свободы 2. Распределение Стьюдента (t-распределение). Пусть случайная величина
имеет распределение Стьюдента, или t -распределение. С увеличением k- распределение также стремится к нормальному закону 3. Распределение Фишера(F-распределение). Пусть X и Y независимые случайные величины, распределенные по закону
имеет распределение Фишера, или F- распределение со степенями свободы k 1 и k 2. С увеличением k 1 и k 2 F- распределение стремится к нормальному закону. Контрольные вопросы 1. Как находится плотность распределения случайной величины Y, если эта случайная величина есть монотонная функция случайной величины X, закон распределения которой известен? 2. Как находится закон распределения немонотонной функции одного случайного аргумента? 3. Как определяется закон распределения функции двух случайных аргументов? 4. Что означает произвести композицию двух законов распределения? 5. Как определяется математическое ожидание функции случайного аргумента, закон распределения которого известен? 6. Сформулируйте и докажите теорему о математическом ожидании суммы двух случайных величин. 7. Сформулируйте и докажите теорему о математическом ожидании произведения двух случайных величин. 8. Чему равно математическое ожидание от произведения нескольких независимых случайных величин? 9. Как определяется дисперсия функции одного случайного аргумента (нескольких аргументов), если известен только закон распределения аргумента (аргументов)? 10. Сформулируйте и докажите теорему о дисперсии суммы случайных величин. 11. Чему равна дисперсия суммы некоррелированных случайных величин? 12. Сформулируйте и докажите теорему о дисперсии произведения двух независимых случайных величин. 13. Сформулируйте свойства корреляционного момента. 14. Чему равен коэффициент корреляции случайных величин, связанных между собой линейной зависимостью? 15. Функция каких случайных величин имеет распределение Хи -квадрат, Стьюдента, Фишера?
|

 . Пусть
. Пусть  – независимые случайные величины, распределенные по нормальному закону, причем
– независимые случайные величины, распределенные по нормальному закону, причем  ,
,  , т.е. случайные величины
, т.е. случайные величины  степенями свободы, т.е.
степенями свободы, т.е. 
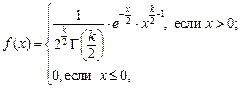
 – гамма функция.
– гамма функция. – распределение стремится к нормальному закону.
– распределение стремится к нормальному закону.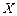 имеет нормированное нормальное распределение, т.е.
имеет нормированное нормальное распределение, т.е.  ,
,  .
.  – независимая от X случайная величина распределена по закону
– независимая от X случайная величина распределена по закону