Неравенство Чебышева. Великий русский математик, академик П.Л
Великий русский математик, академик П.Л. Чебышев в 1846 г. вывел простое неравенство, позволяющее доказать закон больших чисел в самой общей форме. Рассмотрим случайную величину X, математическое ожидание которой Неравенство Чебышева утверждает: вероятность того, что отклонение случайной величины X от её математического ожидания будет по абсолютной величине не менее любого числа
Доказательство. 1. Пусть случайная величина X дискретная с рядом распределения
Тогда дисперсия случайной величины X
Все слагаемые этой суммы неотрицательны. Отбросим все слагаемые, у которых
т.е. суммирование распространяется только на значения i, для которых Заменим в формуле (5.3) выражение
так как
Подставляя в формулу (5.4) данное выражение, получим
Откуда непосредственно вытекает неравенство (5.1). 2. Пусть теперь случайная величина X непрерывна с плотностью распределения
Возможные значения случайной величины принадлежат всей числовой оси. Выделим на числовой оси вправо и влево от математического ожидания отрезки длиной ε (рис. 5.1) ε ε
A а B Рис. 5.1 Если в выражении (5.5) интеграл по всей оси ОХ заменим интегралом по области, лежащей вне отрезка АВ, то величина интеграла при этом может только уменьшиться, поскольку под интегралом стоит неотрицательная функция, т.е.
Заменяя
Так как
то неравенство (5.7) принимает вид:
Здесь знак Неравенство Чебышева может быть записано и в другой форме, применительно к противоположному событию:
Неравенство Чебышева имеет для практики ограниченное значение, так как дает грубую оценку. Это неравенство полезно лишь при относительно больших ε. Теоретическое же значение очень велико.
|

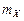 и дисперсия
и дисперсия 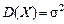 .
.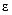 > 0, ограничено сверху величиной
> 0, ограничено сверху величиной 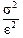 , т.е.
, т.е.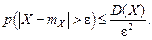 (5.1)
(5.1)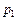
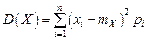 . (5.2)
. (5.2)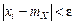 , вследствие чего сумма (5.2) может только уменьшиться:
, вследствие чего сумма (5.2) может только уменьшиться: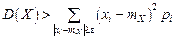 , (5.3)
, (5.3)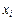 отклоняется от математического ожидания
отклоняется от математического ожидания 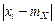 через ε, от такой замены сумма только уменьшится:
через ε, от такой замены сумма только уменьшится: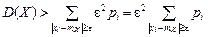 , (5.4)
, (5.4)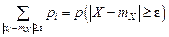 .
.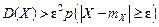 .
.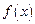 . Тогда
. Тогда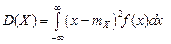 .
.  (5.5)
(5.5)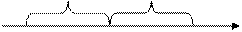
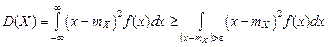 . (5.6)
. (5.6)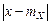 под интегралом (5.6) через ε, снова можем только уменьшить величину интеграла.
под интегралом (5.6) через ε, снова можем только уменьшить величину интеграла.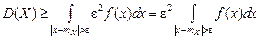 . (5.7)
. (5.7)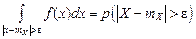 ,
,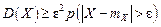 . (5.8)
. (5.8)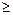 заменен знаком >, так как для непрерывной случайной величины вероятность точного равенства равна нулю.
заменен знаком >, так как для непрерывной случайной величины вероятность точного равенства равна нулю.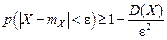 . (5.9)
. (5.9)


