Теорема Чебышева
Пусть
Введем новую случайную величину:
Теорема Чебышева. При неограниченном увеличении числа наблюдаемых испытаний среднее арифметическое наблюдаемых значений случайной величины, имеющей конечную дисперсию, сходится по вероятности к её математическому ожиданию, т.е.
Доказательство. Найдем числовые характеристики случайной величины
Применим теперь неравенство Чебышева в виде формулы (5.3) к случайной величине
Подставляя в формулу (5.11), получим
В пределе при Определим смысл формулировки «сходимость по вероятности». Пусть на некотором вероятностном пространстве заданы последовательность случайных величин
или
Сходимость по вероятности отличается от сходимости в смысле обычного анализа. Разница между указанными видами сходимости состоит в следующем: если Пусть Пример 1. Сколько надо провести измерений данной величины, чтобы с вероятностью не менее 0,95 гарантировать отклонение средней арифметической этих измерений от истинного значения величины не более чем на 1, если среднее квадратичное отклонение каждого из измерений не превосходит 5? Р е ш е н и е. Пусть Необходимо найти n, при котором
Ответ: потребуется не менее 500 измерений. Теорема Чебышева может быть распространена на более общий случай, когда характеристики наблюдаемой случайной величины меняются от опыта к опыту. В этом случае имеет место следующая обобщенная теорема Чебышева: при неограниченном увеличении числа независимых испытаний над случайными величинами, имеющими ограниченные дисперсии, среднее арифметическое наблюдаемых значений сходится по вероятности к среднему арифметическому математических ожиданий этих величин, т.е.
где
причем Доказательство теоремы нужно произвести самостоятельно.
|

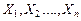 – последовательность попарно независимых случайных величин с одинаковыми математическими ожиданиями и ограниченными дисперсиями, т.е.
– последовательность попарно независимых случайных величин с одинаковыми математическими ожиданиями и ограниченными дисперсиями, т.е.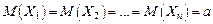 ;
;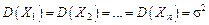 .
.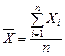 . (5.10)
. (5.10)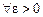
 . (5.11)
. (5.11)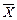 . Пользуясь свойствами числовых характеристик, получим:
. Пользуясь свойствами числовых характеристик, получим: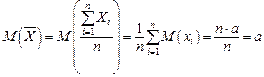 ;
;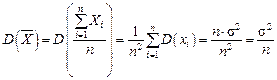 .
.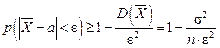 . (5.12)
. (5.12)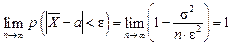 .
.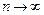 величина
величина 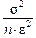 стремится к нулю, и, следовательно, получаем доказываемую формулу (5.11).
стремится к нулю, и, следовательно, получаем доказываемую формулу (5.11).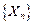 и случайная величина X, т.е.
и случайная величина X, т.е. 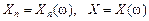 . Последовательность
. Последовательность 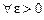
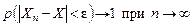
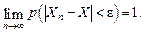
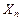 стремится при
стремится при 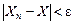 ; если же
; если же 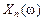 стремится при
стремится при 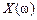 при всех
при всех 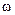 , более того может быть, что
, более того может быть, что 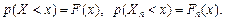 Говорят, что
Говорят, что 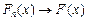 в каждой точке непрерывности
в каждой точке непрерывности 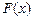 .
.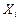 – результат i -го измерения
– результат i -го измерения 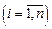 ; a – истинное значение величины, т.е.
; a – истинное значение величины, т.е.  .
.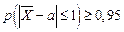 , где по условию ε=1;
, где по условию ε=1; 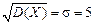 . Используем формулу (5.12)
. Используем формулу (5.12)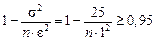 , откуда
, откуда 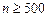 .
.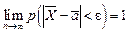 , (5.13)
, (5.13)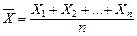 ;
; 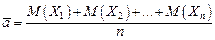 ,
,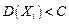 ,
, 


