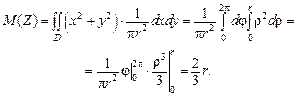Математическое ожидание функции случайных величин
Пусть
Если X – непрерывная случайная величина, тогда
где Аналогично может быть определено математическое ожидание функции от двух случайных аргументов
Для дискретных случайных величин:
Для непрерывных случайных величин:
где Теорема 1. Математическое ожидание суммы как зависимых, так и независимых двух случайных величин равно сумме математических ожиданий этих величин:
Теорема 2. Математическое ожидание произведения случайных величин равно произведению их математических ожиданий плюс корреляционный момент:
Следствие. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
Пример 1. Найти математическое ожидание случайной величины
Р е ш е н и е. По формуле (4.10) имеем:
Пример 2. Система Р е ш е н и е. Система
По формуле (4.12)
Таким образом, искомое математическое ожидание равно 2/3 r.
|
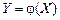, где X – дискретная случайная величина с возможными значениями 
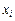и вероятностями 
, 
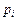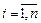, тогда математическое ожидание случайной величины Y можно определить по формуле:
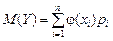. (4.9)
, (4.10)
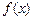– плотность распределения случайной величины X.
.
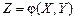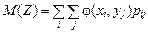. (4.11)
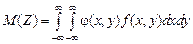, (4.12)
– плотность распределения системы 
.
(4.13)
(4.14)
(4.15)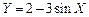
, если плотность распределения случайной величины X имеет вид:
