Зависимые и независимые случайные величины. Условные законы распределения и условные числовые характеристики
При изучении системы случайных величин зависимость меж- Случайные величины X и Y называются независимыми, если
Для дискретных случайных величин X и Y это требование эквивалентно равенству
где
Если случайные величины X и Y зависимы, то необходимо ввести понятие условного закона распределения и условной плотности распределения. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определенное значение, называется условным законом распределения. Для двумерной дискретной случайной величины (X, Y), принимающей значения (
или
т.е.
По аналогии
Для непрерывных случайных величин аналогичным образом определяется условная плотность распределения:
Условная плотность распределения обладает всеми свойствами безусловной плотности распределения. В случае независимости случайных величин X и Y все условные плотности распределения совпадают с безусловными, т.е.
И наоборот, различие условных и безусловных плотностей распределения означает зависимость случайных величин. Для зависимых случайных величин вводятся понятия условных числовых характеристик. Условное математическое ожидание в дискретном случае:
Условное математическое ожидание в непрерывном случае:
Условная дисперсия в дискретном и непрерывном случае имеет вид:
Из определения условных математических ожиданий следует, что В качестве количественной характеристики степени зависимости случайных величин X и Y часто используют коэффициент корреляции 1) 2) если 3) если Х и Y независимы, то Пример 1. Плотность распределения системы случайных величин (X, Y) имеет вид:
Определить, зависимы или независимы составляющие X и Y. Р е ш е н и е. Вычислим плотности распределения составляющих, используя формулы (3.9) и (3.10) при
Таким образом,
Случайные величины X и Y независимы, так как выполняется условие (3.14):
Пример 2. Плотность распределения двухмерной случайной величины
Определить: а) зависимы или независимы составляющие X и Y; б) условные математические ожидания и условные дисперсии. Р е ш е н и е. а) Плотность распределения составляющей X по формуле (3.9)
Аналогично для составляющей Y по формуле (3.10):
Очевидно, что условие (3.14) не выполняется. Таким образом, X и Y зависимы. б) Найдем сначала условные плотности распределения
Найдем условные математические ожидания по формулам (3.18):
Аналогично
Найдем условную дисперсию по формуле (3.19):
Аналогично
Пример 3. Закон распределения дискретной двумерной случайной величины Таблица 3.3
Найти: а) закон распределения составляющих X и Y; б) условные законы распределения случайной величины X при условии Y = 2 и случайной величины Y при условии X = 1; в) вычислить Р е ш е н и е. а) Случайная величина X может принять два значения:
т.е. ее закон распределения представлен рядом распределения:
Контроль: 0,8+0,2=1. Аналогично получаем закон распределения составляющей Y (складываем вероятности по столбцам):
Контроль: 0,2+0,3+0,3+0,2=1. б) Условный закон распределения X при условии Y = 2 получим, если вероятности
Контроль: 0,75 + 0,25 = 1. Для получения условного закона распределения Y (при условии X = 1), вероятности
Контроль: 0,125 + 0,3125 + 0,375 + 0,1875 = 1. в) Для нахождения вероятностей
т.е. складываем вероятности для значений (1,−1), (1,0), (2,−1), (2,1).
|

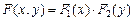 .
.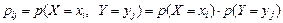 , (3.13)
, (3.13)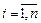 и
и 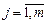 , а для непрерывных случайных величин условие непрерывности равно
, а для непрерывных случайных величин условие непрерывности равно . (3.14)
. (3.14)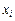 ,
, 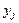 )
) 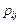 , можно определить условную вероятность
, можно определить условную вероятность 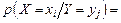
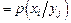 , пользуясь аксиомой умножения:
, пользуясь аксиомой умножения: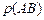 =
= 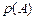 ×
× 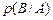
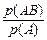 ,
,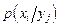 =
= 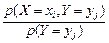 =
= 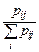 . (3.15)
. (3.15)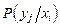 =
= 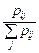 . (3.16)
. (3.16)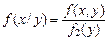 и
и 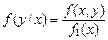 . (3.17)
. (3.17)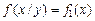 ;
; 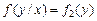 .
.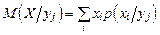 ;
; 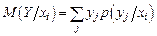 .
.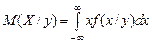 ;
; 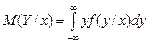 . (3.18)
. (3.18)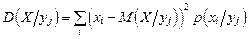 ;
;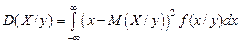 . (3.19)
. (3.19) – это функция от y, а
– это функция от y, а 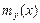 – функция от x. Причем, если система случайных величин
– функция от x. Причем, если система случайных величин 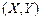 непрерывна, то функции
непрерывна, то функции 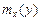 и
и 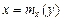 и
и 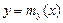 называются уравнениями регрессии X по Y
называются уравнениями регрессии X по Y  называется линиями регрессии.
называется линиями регрессии. (см. формулу (3.12)), но он характеризует лишь степень линейной зависимости. Это следует из его свойств:
(см. формулу (3.12)), но он характеризует лишь степень линейной зависимости. Это следует из его свойств: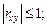
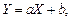 где a и b = const, то
где a и b = const, то 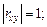
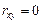 .
.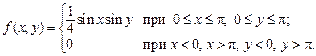
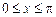 и
и 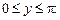
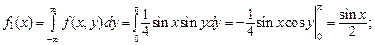
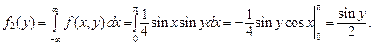
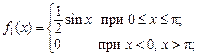
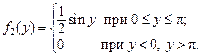
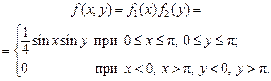

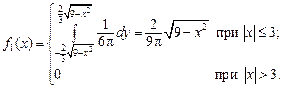
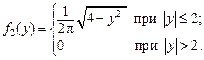
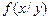 и
и  по формулам (3.17):
по формулам (3.17):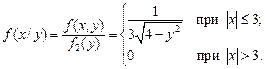
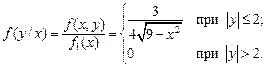
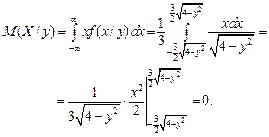
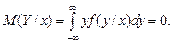
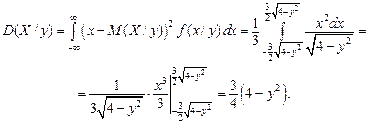
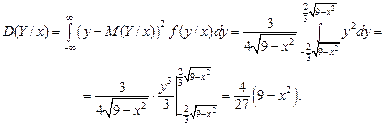
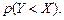
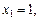
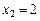 с вероятностями (складываем вероятности по строкам):
с вероятностями (складываем вероятности по строкам):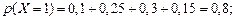
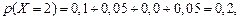
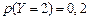 . Получим
. Получим :
: складываем вероятности событий
складываем вероятности событий 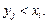 Получим:
Получим: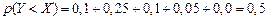 ,
,


