Закон распределения системы двух случайных величин
Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях. Так же как и для одной случайной величины, закон распределения системы может быть задан в различных формах. Рассмотрим сначала таблицу распределения системы дискретных случайных величин. Пусть (X, Y) – двумерная дискретная случайная величина, возможные значения которой Распределение системы (X, Y) показано в табл. 3.1, которая называется таблицей распределения системы двух дискретных случайных величин. Таблица 3.1
Все возможные события
При этом
Пример. По цели производится два выстрела. Вероятность попадания при одном выстреле равна 0,7. Найти распределение двумерной случайной величины (X, Y), считая X – число попаданий, Y – число промахов. Р е ш е н и е. Возможные значения случайных величин X и Y одинаковы и равны 0, 1, 2. Тогда
Таким образом, получена таблица распределения (табл. 3.2). Таблица 3.2
Контроль:
|

 . Вероятности принятия этих возможных значений
. Вероятности принятия этих возможных значений  , где
, где  , а
, а  .
.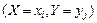 при
при 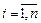 и
и 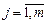 составляют полную группу несовместных событий, поэтому
составляют полную группу несовместных событий, поэтому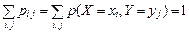 .
.
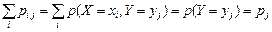 .
. р (Æ) = 0;
р (Æ) = 0;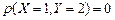 ;
; ;
;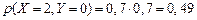 ;
;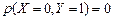 ;
;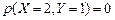 ;
; ;
; .
. , т.е. сумма вероятностей равна 1.
, т.е. сумма вероятностей равна 1.


