Равномерное и нормальное распределение на плоскости
Система двух независимых случайных величин (X, Y) имеет равномерное распределение в области D плоскости XOY, если плотность распределения системы в точках плоскости XOY имеет вид:
Система независимых случайных величин (X,Y) имеет нормальное распределение на плоскости, если плотность распределения системы имеет вид:
Если Если Вероятность попадания случайной точки (X, Y) в прямоугольник со сторонами, параллельными осям координат для распределения (3.20), можно вычислить по формуле:
Плотность нормального распределения для системы двух зависимых случайных величин X и Y выражается формулой:
т.е. определяется пятью параметрами: Контрольные вопросы 1. Что называется системой случайных величин? 2. Как можно трактовать систему случайных величин? 3. Что называется законом распределения системы двух случайных величин? 4. Дайте определение функции распределения системы двух случайных величин и укажите ее свойства. 5. Дайте определение плотности распределения вероятностей системы двух случайных величин и укажите ее свойства. 6. Что называется условным законом распределения? 7. Как выражается плотность распределения каждой из величин, входящих в систему, через плотность распределения системы? 8. Какие случайные величины называются зависимыми? 9. Что является необходимым и достаточным условием независимости случайных величин? 10. Что называется корреляционным моментом? Коэффициентом корреляции? 11. Чему равен коэффициент корреляции для независимых случайных величин? 12. Какие случайные величины называются некоррелированными? 13. Следует ли из некоррелированности случайных величин их независимость, и наоборот? 14. Как записывается формула для плотности распределения равномерно распределенной в области D системы двух независимых случайных величин? 15. Как записывается формула для плотности распределения нормально распределенной системы двух независимых и зависимых случайных величин?
|

 (3.20)
(3.20)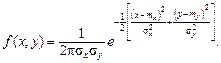 (3.21)
(3.21)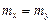 , то получим каноническую форму нормального распределения на плоскости.
, то получим каноническую форму нормального распределения на плоскости. , то нормальное распределение независимых случайных величин называется распределением Рэлея, которое распространено в стрельбе, радиофизике, электронике.
, то нормальное распределение независимых случайных величин называется распределением Рэлея, которое распространено в стрельбе, радиофизике, электронике.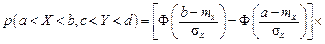
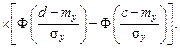
 ,
,
 ,
,  .
.


