Плотность распределения системы двух случайных величин
Плотность распределения является исчерпывающей характеристикой системы непрерывных случайных величин, с помощью которой описание распределения системы становится более наглядным. Пусть имеется система двух непрерывных случайных величин. Рассмотрим вероятность попадания случайной точки
Разделим полученную вероятность на площадь этого прямоугольника и перейдем к пределу при
Предположим, что функция
Функция Геометрически плотность распределения системы двух случайных величин
Рис. 3.2 Рис. 3.3 Имеют место следующие свойства: 1. Плотность распределения есть функция неотрицательная:
2. Двойной несобственный интеграл в бесконечных пределах от плотности распределения системы равен единице:
3. Функция распределения непрерывной двумерной случайной величины может быть выражена через ее плотность распределения
4. Функция распределения случайных величин
5. Плотность распределения одномерных случайных величин X и Y, составляющих систему, можно выразить формулами:
6. Вероятность попадания непрерывной двумерной случайной величины
равна объему цилиндрического тела, ограниченного сверху поверхностью распределения
|

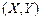 в элементарный прямоугольник со сторонами
в элементарный прямоугольник со сторонами 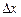 и
и 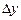 (рис. 3.2). Применяя формулу (3.3), получим:
(рис. 3.2). Применяя формулу (3.3), получим: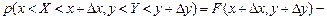
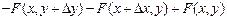 .
. и
и  :
: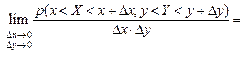
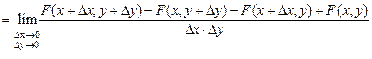 . (3.4)
. (3.4)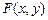 дважды дифференцируема, тогда правая часть формулы (3.4) представляет собой вторую смешанную производную функции
дважды дифференцируема, тогда правая часть формулы (3.4) представляет собой вторую смешанную производную функции  :
: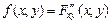 . (3.5)
. (3.5)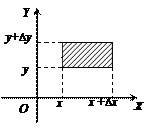

 .
. . (3.6)
. (3.6) . (3.7)
. (3.7)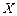 и
и  , составляющих систему
, составляющих систему 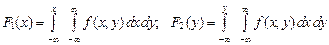 . (3.8)
. (3.8)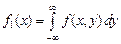 ; (3.9)
; (3.9)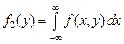 . (3.10)
. (3.10) ,
,


