Закон распределения функции двух случайных величин
Пусть случайная величина Z является функцией двух случайных величин, т.е.
Пусть
где Если X и Y независимы, то
тогда
Следует отметить, что значения Z однозначно определяются значениями X и Y. Пример 1. Дискретные случайные величины X, Y заданы распределениями:
Составить распределение случайной величины Р е ш е н и е. Составим возможные значения Z:
Найдем вероятности этих возможных значений:
Таким образом, искомое распределение:
Пример 2. Случайная точка
откуда
Таким образом, искомая плотность распределения равна 1/π(1+ z 2).
|
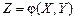. (4.6)
плотность распределения системы величин 
, тогда плотность распределения случайной величины 
определяется равенством: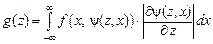
, (4.7)
обратная функция к функции (4.6).
,
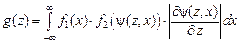. (4.8)
; 
.
.
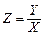Р е ш е н и е. В данном случае функция распределения случайной величины Z есть относительная площадь области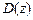 
(рис. 4.1):
,
.
