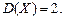Корреляционный момент функций случайных величин и его свойства
Согласно определению корреляционного момента двух случайных величин X и Y, имеем:
Раскрывая скобки и применяя свойства математического ожидания, получим:
Рассмотрим две функции
Согласно формуле (4.30)
Рассмотрим основные свойства корреляционного момента Свойство 1. От прибавления к случайным величинам постоянных величин корреляционный момент и коэффициент корреляции не меняются. Свойство 2. Для любых случайных величин X и Y абсолютная величина корреляционного момента не превосходит среднего геометрического дисперсий случайных величин:
где Свойство 3. Если
Пример. Имеются две случайные величины X и Y, связанные соотношением Р е ш е н и е. По формуле (4.30):
Рассмотрим распределение случайных величин, являющихся функцией случайных величин, которые находят широкое применение в математической статистике.
|
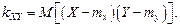
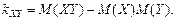(4.30)
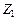и 
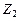системы двух случайных величин 
:
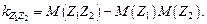(4.31)
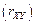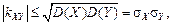
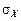и коэффициента корреляции 
.
и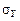 
– средние квадратичные отклонения случайных величин X и Y.
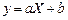, то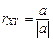
.
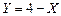. Найти корреляционный момент, если 
, 
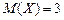