Закон распределения функции одной случайной величины
Одной из важных задач в теории вероятностей является определение закона распределения функции одной или нескольких случайных величин, если известны распределения одного или нескольких аргументов. Такие функции тоже являются случайными величинами. Примерами простейших функций случайных величин являются:
Начнем рассмотрение с наиболее простой задачи о законе распределения функции одного случайного аргумента, т.е.
Пусть дискретная случайная величина X имеет ряд распределения:
тогда случайная величина Y будет также дискретной случайной величиной с рядом распределения:
где Если все значения
Если же среди Пример 1. Дана дискретная случайная величина X рядом распределения:
Найти закон распределения случайной величины Р е ш е н и е. Возможные значения случайной величины Y:
Ряд распределения случайной величины Y:
или
Пусть теперь случайная величина X является непрерывной случайной величиной с плотностью распределения Пусть Так как Найдем сначала функцию распределения случайной величины Y, т.е.
Дифференцируя полученный интеграл по y, получим плотность распределения случайной величины, заданной по формуле (4.1):
В случае убывающей функции
так как в этом случае Объединяя (4.2) и (4.3), получим
Пример 2. Случайная величина X распределена нормально ( Р е ш е н и е. Так как случайная величина X имеет нормальное распределение с параметрами
Функция Обратная функция по отношению к функции
ее производная
Следовательно,
Если обратная функция неоднозначная, т.е. одному значению величин Y соответствует несколько значений аргумента
где n – число участков, на которых функция (4.1) изменяется монотонно, то формула (4.4) принимает вид:
Пример 3. Случайная величина X имеет нормальное распределение с параметрами Р е ш е н и е. Обратная функция
Применяя формулу (4.5), получим:
Итак,
Получили плотность распределения случайной величины
|

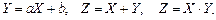
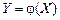 . (4.1)
. (4.1)
 различны, то для каждого
различны, то для каждого 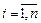 события {
события { 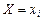 } и {
} и { 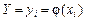 } тождественны, поэтому
} тождественны, поэтому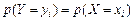 .
. .
.
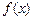 . Найдем плотность распределения случайной величины, заданной формулой (4.1).
. Найдем плотность распределения случайной величины, заданной формулой (4.1). монотонно возрастающая функция.
монотонно возрастающая функция.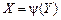 .
. :
: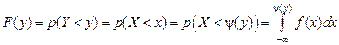 .
.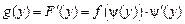 . (4.2)
. (4.2)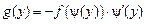 , (4.3)
, (4.3)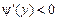 .
. . (4.4)
. (4.4) ). Найти закон распределения случайной величины
). Найти закон распределения случайной величины 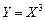 .
. , то ее плотность распределения имеет вид:
, то ее плотность распределения имеет вид: .
.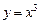 монотонна на (
монотонна на ( ), поэтому можно применить формулу (4.4).
), поэтому можно применить формулу (4.4). ,
,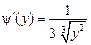 .
.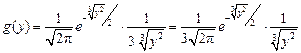 .
. , которые обозначим:
, которые обозначим:
 . (4.5)
. (4.5)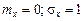 . Найти распределение случайной величины
. Найти распределение случайной величины 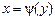 неоднозначная. Одному значению
неоднозначная. Одному значению 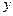 соответствуют два значения функции x:
соответствуют два значения функции x: ,
, 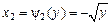 .
. .
. .
.


