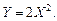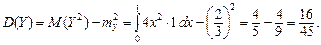Дисперсия функции случайных величин
Для функции одного случайного аргумента
дисперсия выражается формулой:
Выражение (4.17) показывает, что дисперсия функции случайных величин определяется как математическое ожидание некоторой новой функции, поэтому вычисление дисперсии может быть осуществлено приемами, совершенно аналогичными рассмотренным в предыдущем разделе. Если X – дискретная случайная величина, то дисперсия выражается суммой:
а если X – непрерывная случайная величина, то дисперсия функции выражается интегралом:
где Аналогично выражается дисперсия функции двух случайных величин:
В дискретном случае:
где В непрерывном случае:
где Заметим, что при вычислении дисперсии удобно бывает пользоваться формулой:
В таком случае формулы (4.18), (4.19), (4.21) и (4.22) можно заменить следующими:
Теорема 1. Дисперсия суммы двух случайных величин равна сумме дисперсий этих величин плюс удвоенный коэффициент корреляции:
Следствие. Дисперсия суммы некоррелированных
Теорема 2. Дисперсия произведения двух независимых случайных величин вычисляется по формуле:
Пример. Случайная величина X подчинена равномерному закону распределения в интервале (0,1). Найти дисперсию случайной величины Р е ш е н и е. Случайная величина X имеет плотность распределения:
Найдем сначала математическое ожидание случайной величины
Дисперсия по формуле (4.24):
Таким образом, искомая дисперсия равна 16/45.
|

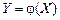 (4.16)
(4.16)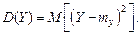 (4.17)
(4.17) (4.18)
(4.18)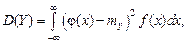 (4.19)
(4.19)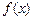 – плотность распределения случайной величины X.
– плотность распределения случайной величины X.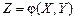 . (4.20)
. (4.20) , (4.21)
, (4.21) – возможные значения системы (Х, Y), а
– возможные значения системы (Х, Y), а 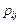 – вероятность принятия этих значений.
– вероятность принятия этих значений.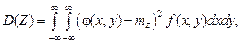 (4.22)
(4.22) – плотность распределения системы (X, Y);
– плотность распределения системы (X, Y);  – математическое ожидание функции (4.20).
– математическое ожидание функции (4.20).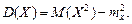
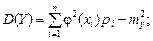 (4.23)
(4.23)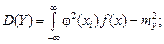 (4.24)
(4.24) (4.25)
(4.25) (4.26)
(4.26)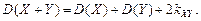 (4.27)
(4.27)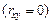 случайных величин равна сумме их дисперсий:
случайных величин равна сумме их дисперсий: . (4.28)
. (4.28)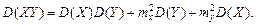 (4.29)
(4.29)