Функция распределения системы двух случайных величин
Функцией распределения системы двух случайных величин называется функция двух аргументов
Для дискретной двумерной случайной величины функция распределения определяется по формуле:
Отметим свойства функции распределения. 1. Функция распределения
2. Функция распределения при при 3. Если хотя бы один из аргументов обращается в бесконечность, функция распределения
4. Если один из аргументов обращается в бесконечность, функция распределения
где
5. Если оба аргумента равны + ¥, то функция распределения равна единице:
6. Вероятность попадания случайной точки
7. Вероятность попадания случайной точки
где стороны прямоугольника параллельны координатным осям.
|
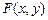, равная вероятности совместного выполнения двух неравенств 
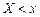и 
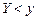, т.е.
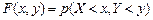. (3.1)
Геометрически функция распределения системы двух случайных величин представляет собой вероятность попадания случайной точки (x, y) в левый нижний бесконечный квадрант плоскости (рис. 3.1) с вершиной в точке (X, Y) (заштрихованная область).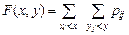
. (3.2)
.
;
.
.
;
,
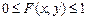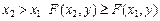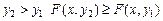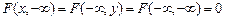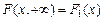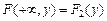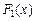и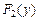 
– функции распределения случайных величин X и Y, т.е.
.
.
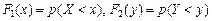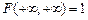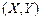в полуполосу равна приращению функции распределения по одному аргументу
;
.
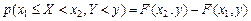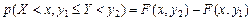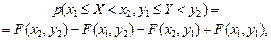(3.3)
