Основные числовые характеристики системы двух случайных величинВ основу получения числовых характеристик системы случайных величин положено понятие моментов. Как и для одной случайной величины, это начальные и центральные моменты. Формулы для вычисления начальных моментов для системы дискретных случайных величин
для системы непрерывных случайных величин
В частности, начальные моменты первого порядка
определяют на плоскости Формулы вычисления центральных моментов: в дискретном случае:
в непрерывном случае:
Центральными моментами второго порядка являются дисперсии
характеризующие рассеивание случайной точки в направлении осей Ох и Oy. Важную роль при исследовании системы двух случайных величин играет второй смешанный центральный момент
В дискретном случае формула (3.11) выражается суммой:
а в непрерывном – интегралом:
Применяется еще одна характеристика, называемая коэффициентом корреляции (
где
|
записываются следующим образом:
;
.
; 
,
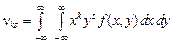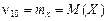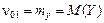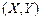точку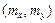 
, называемую центром рассеивания системы.
;
.
,
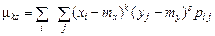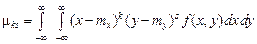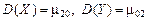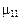, который называется корреляционным моментом, моментом связи и еще ковариацией величин X и Y,для него приняты обозначения 
или 
:
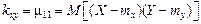. (3.11)
,
.
):
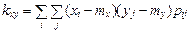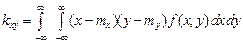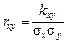, (3.12)
, 
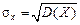– положительные квадратные корни из дисперсии.
