Теорема Бернулли
Теорема Бернулли является одной из первых форм закона больших чисел. Она устанавливает связь между частотой события и его вероятностью. Теорема Бернулли. При неограниченном увеличении числа независимых опытов в постоянных условиях частота рассматриваемого события A сходится по вероятности к его вероятности p в отдельном опыте. Обозначим частоту события A через
Доказательство. Обозначим через
где q= 1– p. Каждая из величин Следовательно, для каждой величины
Частота появления A в n опытах равна Можно применить теорему Чебышева, так как случайные величины Xi попарно независимы (опыты независимые), математические ожидания равны, дисперсии ограничены (можно доказать, что pq<;1/4). По теореме Чебышева получим
что и требовалось доказать. Обобщением теоремы Бернулли на случай, когда опыты происходят при неодинаковых условиях, является теорема Пуассона. Теорема Пуассона. При неограниченном увеличении числа опытов в переменных условиях частота события сходится по вероятности к средним арифметическим его вероятностей
где Доказательство. Пусть случайные величины Xi – число появлений события A в i- м испытании
Следовательно, для каждой случайной величины
Обозначим частоту события A через
тогда
Можно применить обобщенную теорему Чебышева, так как
Теорема доказана.
|
, т.е. 
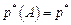, тогда теорему Бернулли можно записать в виде:
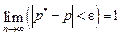. (5.14)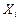
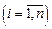число появлений события A в i -м опыте. Величины 
;
.
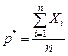– среднему арифметическому наблюдаемых значений.
,
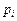, т.е.
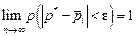, (5.15)
– среднее арифметическое вероятностей.
.
; 
.
,
;
.
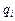
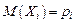при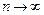 
, т.е.
.
