Двумерные случайные величины.Опр. Вектор Z=(x,y) компоненты Х и У которые яв-ся случ-ми величинами назыв-ся случайным вектором, или двумерной случайной величиной. Например: X-рост чел-ка; У-вес чел-ка ß это двумерные непрерывные величины. Рез-т им-я двумерной случ. величины- это точка плоскости. Опр. Связь между переменными назыв. статистической, если каждому значению одной переменной ставится в соответствие закон распределения другой. Задание статистической связи между двумя переменными равносильна заданию двумерной случайной величины. Рассмотрим двумерные дискретные случ. величины закона распределения, в данном случае задаётся с помощью таблицы вида:
Xi | * * | *ß Совместный закон распределения случ-х величинин. Xi***********************Pij Основное св-во совместного закона распределения
|
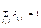Опр. Закон распределения одной переменной при фикс-ом значении др-ой назыв.ус-ным распределением. Опр.: Связь между переменными наз-ся функциональной, если каждому значению одной переменной ставится в соответствие однозначно определенное значение другой переменной. Опр.: Функциональная зависимость между значениями одной переменной и усл-ми матам-ми ожиданиями другой назыв. корреляционной. Корреляция бывает двух видов: а) (xi, Mxi (Y))- корреляционная зависимость у по х; б) (Myj(X)yj)- коррел. зависимость х по у. Опр. Ф-я j=j(х,у)- назыв. плотностью распределения двумерной случайной величины Z, если для произвольных чисел a, b, g, d (a<b, g<d) вер-ть того, что значения случ-ой величины Z окажется принадлежащим прямоуг-ку a£Х£b, g£Y£d вычисл-ется по ф-ле: 
; 
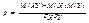, где а величина 
