Центральная предельная теорема Муавра Лапласа как следствие из неё.
Т. Пусть случ. величины Х1,Х2,…Хn- независимы и одинаково распределены, тогда закон распределения их суммы (т.е. случ. величины Х=Х1+Х2+…+Хn) неограниченно приближаются к нормальному при неограниченном увеличении n.; Следствие: Биномиальное распределение переходит в нормальное при неограниченном увеличении n.; Док-во: Пусть Х биномиально распределена с параметрами n и p. Пусть более точно Х- число наступления события А в n повторных независимых испытаниях в каждом из которых событие А наступ. с вер-тью р, тогда Х=Х1+Х2+…+Хn, где Хi-число наст-ий соб-ия А в i-ом испытании (i=1,2,…n). Хi- независ. и одинаково распределены по центральной предел-ой теореме. Следствие доказано.; Пусть X=m- биномиально распределена с параметрами n и p => для нормального распр-ия известно, что вер-ть попадания в отрезок.
теорема Муавра Лапласа.
|
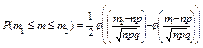-Интегральная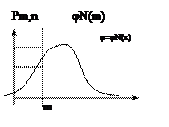
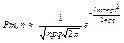- Локальная теорема Муавра Лапласа
