Опр.: Пусть закон распределения случ. величины Х имеет вид:
Х:
| xi
| x1
| x2
| …
| xk
|
| pi
| p1
| p2
| …
| pk
|
Дисперсией D(X)- этой случ. величины называется число, вычисл. по ф-ле: 
Неформально: Дисперсия случ. величины яв-ся мерой разброса значений этой случ. величины около её мат. ожидания. Св-ва дисперсии: 1)D(С)=0, С- пост. случ. величина. 2)D(aX)=aв квадрате×D(X). 3)Пусть случ. величины X иY-незави-симы =>D(X±Y)=D(X)+D(Y). 4)D(X)=M(X в квадрате) – М в квадрате(Х). 5)Пусть случ. величины Х1,Х2,…Хn- независимы и D(X1)=…=D(Xn)=s в квадрате.; тогда D((x1+…+xn)/n)=(s в квадрате)/n). Замечание: 
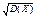– назыв. среднеквадратическим отклонением случ. величины X и часто обозначается через s(сигма). 
Теорема: Пусть случ. величина Х биномиально распределена с параметрами n и p, тогда M(X)=np; D(X)=npq; q=1-p; M(X/n)=p; D(X/n)=(pq)/n. Док-во: Пусть Х- число наступившего события А в n повторн. независ. исп-ях в каждом из которых соб А наступает с вер-тью р => Х=Х1+Х2+…+Хn,где Xi- число наступ-его соб-я А в i испытаний (1£i£n). Х1,Х2,…Хn– независ. и одинаково распределены. 1£i £ n.
M(Xi)=0×q+1×p=p.;
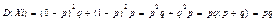M(X)=M(X1+…+Xn)=M(X1)+…+M(Xn)=p+…+p=np. D(X)=D(X1+…+Xn)=D(X1)+…+D(Xn)=pq+..+pq=npq. Теорема доказана. Пример: Пусть Х-бином. Распред-а n=3, p=0,8; M(X)=3×0,8=2,4; D(X)=3×0,8×0,2=0,48.
