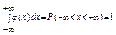Вер-ть того, что знач-ие случ. величины Х окажется принадлежащим некотор. отрезку [a,b] численно равна площади S[a,b] под кривой плотности распред-я j=j(х) на [a,b]. Теорема: (Характеристическое св-во плотности распределения.) Функция j=j(х) яв-ся плотностью распределения некотор. непрерывной случайной величины Х т.и т.т.к. выполняют след. условия. 1)Не отрицательность, т.е. j(х)³0 (при всех Х); 2)Условия нормировки {интеграл от -¥ до +¥}×j(х)dx=1; Док-во: Пусть j(х)- плотность распределения случ. величины Х.
1)Предположим, что j(х)<0 на некотор.[a,b] =>P(a£x£b)= 
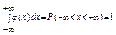
×j(х)dx<0 невозможною => предположение неверно. 2) 
