Опр. Коэффициентом корреляции случ. величин Х и У назыв. число, вычисляемое по ф-ле: r=(M(XY)-M(X)M(Y))/(sXsY), где sX=ÖD(X), sY=ÖD(Y), а M(XY)-M(X)M(Y)- ковариация KXY. Модуль коэфф-та корреляции не превосходит 1, т.е. -1£r£1.; Если модуль коэфф-та |r|=1, то между случайными величинами существует линейная функциональная зависимость.; Пусть r- коэфф-нт корреляции случайных величин X и Y: r=(M(XY)-M(X)M(Y))/(sXsY); Заменяя в последнем выражении входящие величины на их выборочные оценки, получаем формулу для вычисления выборочного коэфф-нта корреляции r: 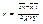
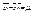 -выборочная ковариация, т.к.
-выборочная ковариация, т.к. 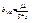 ,
, 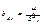 ;
; 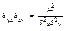 ;
; 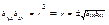 , «+»,если
, «+»,если 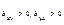 ; «-» если
; «-» если 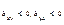 .Если r>0,то связь между переменной называется прямой.Если r<0- связь называется обратной. Связь между переменными признается тесной, если |r|³0,7; умеренной если 0,4£|r|£0,7; слабой если |r|<0,4. Основное св-во коэфф-та корреляции: |r|£1.; Предельное значение коэфф-та корреляции: 1) |r|=1,т.и т.т.к. byx*bxy=1 => прямые регрессии совпадают. 2) r=0 т.и т.т.к. µ=0 ó byx=0 и bxy=0 => прямые регрессии перпендикулярны.; Если r=0 то говорят, что между переменными х и у отсутствует линейная корреляционная зависимость.
.Если r>0,то связь между переменной называется прямой.Если r<0- связь называется обратной. Связь между переменными признается тесной, если |r|³0,7; умеренной если 0,4£|r|£0,7; слабой если |r|<0,4. Основное св-во коэфф-та корреляции: |r|£1.; Предельное значение коэфф-та корреляции: 1) |r|=1,т.и т.т.к. byx*bxy=1 => прямые регрессии совпадают. 2) r=0 т.и т.т.к. µ=0 ó byx=0 и bxy=0 => прямые регрессии перпендикулярны.; Если r=0 то говорят, что между переменными х и у отсутствует линейная корреляционная зависимость.

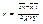
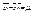 -выборочная ковариация, т.к.
-выборочная ковариация, т.к. 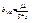 ,
, 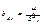 ;
; 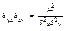 ;
; 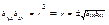 , «+»,если
, «+»,если 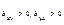 ; «-» если
; «-» если 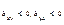 .Если r>0,то связь между переменной называется прямой.Если r<0- связь называется обратной. Связь между переменными признается тесной, если |r|³0,7; умеренной если 0,4£|r|£0,7; слабой если |r|<0,4. Основное св-во коэфф-та корреляции: |r|£1.; Предельное значение коэфф-та корреляции: 1) |r|=1,т.и т.т.к. byx*bxy=1 => прямые регрессии совпадают. 2) r=0 т.и т.т.к. µ=0 ó byx=0 и bxy=0 => прямые регрессии перпендикулярны.; Если r=0 то говорят, что между переменными х и у отсутствует линейная корреляционная зависимость.
.Если r>0,то связь между переменной называется прямой.Если r<0- связь называется обратной. Связь между переменными признается тесной, если |r|³0,7; умеренной если 0,4£|r|£0,7; слабой если |r|<0,4. Основное св-во коэфф-та корреляции: |r|£1.; Предельное значение коэфф-та корреляции: 1) |r|=1,т.и т.т.к. byx*bxy=1 => прямые регрессии совпадают. 2) r=0 т.и т.т.к. µ=0 ó byx=0 и bxy=0 => прямые регрессии перпендикулярны.; Если r=0 то говорят, что между переменными х и у отсутствует линейная корреляционная зависимость.


