ДСВ Х = m имеет геометрическое распределение с параметром p, если она принимает значения 1, 2, …, m, …(бесконечное, но счетное мн-во значений) с вероятностями P(X=m) = pqm-1, где 0<p<1, а q = 1 – p. Ряд геометрич. распределения имеет вид:
| X
|
|
|
| …
| m
| …
|
| p
| p
| pq
| pq2
| …
| pqm-1
| …
|
Определение геометрич. распределения корректно, т.к. 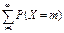 = p + pq + pq2 + …+ pqm-1 = p(1+ q + q2 +…+ qm-1 +…) = p
= p + pq + pq2 + …+ pqm-1 = p(1+ q + q2 +…+ qm-1 +…) = p 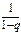 = p/p = 1. СВ Х равная m, имеющая геометрич. распредел., представляет собой число m испытаний, проведенных по схеме Бернулли с вероятностью p наступления события в кажд. испытании до первого положительного исхода. Мат. ожидание СВ Х, имеющей геометрич. распределение с параметром p равно 1/p, а дисперсия равна q/p2.
= p/p = 1. СВ Х равная m, имеющая геометрич. распредел., представляет собой число m испытаний, проведенных по схеме Бернулли с вероятностью p наступления события в кажд. испытании до первого положительного исхода. Мат. ожидание СВ Х, имеющей геометрич. распределение с параметром p равно 1/p, а дисперсия равна q/p2.
ДСВ имеет гипергеометрич. распределение с параметрами n, M, N, если она принимает значения 0, 1, 2, …, min(n, M) с вероятностями P(X= m) = 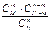 , где
, где 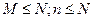 ; n, N, M — натуральные числа. Гипергеометрич. распредел. имеет случ. величина Х = m, число объектов обладающих заданным св-вом среди n объектов, случайно извлеченных без возврата из совокупности N объектов, M из кот. обладают этим св-вом. Мат. ожидание СВ, имеющей гипергеометрич. распредел. с параметрами n, N, M, вычисляется по формуле M(X) =
; n, N, M — натуральные числа. Гипергеометрич. распредел. имеет случ. величина Х = m, число объектов обладающих заданным св-вом среди n объектов, случайно извлеченных без возврата из совокупности N объектов, M из кот. обладают этим св-вом. Мат. ожидание СВ, имеющей гипергеометрич. распредел. с параметрами n, N, M, вычисляется по формуле M(X) = 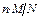 ; D(X) =
; D(X) = 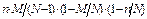 .
.

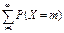 = p + pq + pq2 + …+ pqm-1 = p(1+ q + q2 +…+ qm-1 +…) = p
= p + pq + pq2 + …+ pqm-1 = p(1+ q + q2 +…+ qm-1 +…) = p 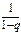 = p/p = 1. СВ Х равная m, имеющая геометрич. распредел., представляет собой число m испытаний, проведенных по схеме Бернулли с вероятностью p наступления события в кажд. испытании до первого положительного исхода. Мат. ожидание СВ Х, имеющей геометрич. распределение с параметром p равно 1/p, а дисперсия равна q/p2.
= p/p = 1. СВ Х равная m, имеющая геометрич. распредел., представляет собой число m испытаний, проведенных по схеме Бернулли с вероятностью p наступления события в кажд. испытании до первого положительного исхода. Мат. ожидание СВ Х, имеющей геометрич. распределение с параметром p равно 1/p, а дисперсия равна q/p2.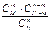 , где
, где 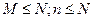 ; n, N, M — натуральные числа. Гипергеометрич. распредел. имеет случ. величина Х = m, число объектов обладающих заданным св-вом среди n объектов, случайно извлеченных без возврата из совокупности N объектов, M из кот. обладают этим св-вом. Мат. ожидание СВ, имеющей гипергеометрич. распредел. с параметрами n, N, M, вычисляется по формуле M(X) =
; n, N, M — натуральные числа. Гипергеометрич. распредел. имеет случ. величина Х = m, число объектов обладающих заданным св-вом среди n объектов, случайно извлеченных без возврата из совокупности N объектов, M из кот. обладают этим св-вом. Мат. ожидание СВ, имеющей гипергеометрич. распредел. с параметрами n, N, M, вычисляется по формуле M(X) = 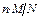 ; D(X) =
; D(X) = 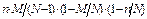 .
.


