Показательным (экспоненциальным) называют распределение вероятностей непрерывной СВ Х, которое описывается функцией плотности вероятности  , где λ>0 постоянна и называется параметром показательного распределения. Примером непрерывн. СВ, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока, где λ – интенсивность потока. Найдем функцию распределения F(x) СВ, распределенной по показательному закону: F(x) =
, где λ>0 постоянна и называется параметром показательного распределения. Примером непрерывн. СВ, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока, где λ – интенсивность потока. Найдем функцию распределения F(x) СВ, распределенной по показательному закону: F(x) =  =
= 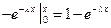 . Итак,
. Итак, 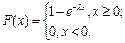
Определим числовые хар-ки СВ, распределенной по показательному закону. Матем. ожидание: M(X) = 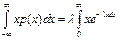 =
=  =
=  . Дисперсия: D(X) =
. Дисперсия: D(X) = 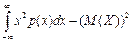 =
= 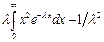 = 2/λ2 – 1/λ2 = 1/λ2. Среднеквадратическое отклонение σ(Х) = 1/λ и, следовательно, совпадает с мат. ожиданием.
= 2/λ2 – 1/λ2 = 1/λ2. Среднеквадратическое отклонение σ(Х) = 1/λ и, следовательно, совпадает с мат. ожиданием.

 , где λ>0 постоянна и называется параметром показательного распределения. Примером непрерывн. СВ, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока, где λ – интенсивность потока. Найдем функцию распределения F(x) СВ, распределенной по показательному закону: F(x) =
, где λ>0 постоянна и называется параметром показательного распределения. Примером непрерывн. СВ, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока, где λ – интенсивность потока. Найдем функцию распределения F(x) СВ, распределенной по показательному закону: F(x) =  =
= 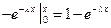 . Итак,
. Итак, 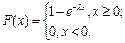
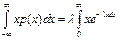 =
=  =
=  . Дисперсия: D(X) =
. Дисперсия: D(X) = 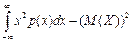 =
= 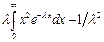 = 2/λ2 – 1/λ2 = 1/λ2. Среднеквадратическое отклонение σ(Х) = 1/λ и, следовательно, совпадает с мат. ожиданием.
= 2/λ2 – 1/λ2 = 1/λ2. Среднеквадратическое отклонение σ(Х) = 1/λ и, следовательно, совпадает с мат. ожиданием.


