ДСВ Х, кот. может принимать только целые неотрицат. значения с вероятностями Pm = P(X=m) = 
, называется распределенной по закону Пуассона с параметром распределения λ, где λ=np. В отличие от биномиальн. распределения здесь СВ может принимать бесконечное мн-во значений, представляющ. собой бесконечн. последовательность целых чисел(0, 1, 2, 3, … и т.д.). Закон Пуассона описывает число событий m, происходящ. за одинаковые промежутки времени. При этом полагается, что события появляются независимо друг от друга с постоянной средней интенсивностью, кот. характеризуется параметром λ=np. Ряд распределения закона Пуассона имеет вид:
| X
|
|
|
| …
| m
| …
|
| p
| e—λ
| λ e—λ
| (λ2 e—λ)/2!
| …
| (λm e—λ)/m!
| …
|
Определение закона Пуассона корректно, т.к.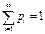 
выполнена. Действительно функцию ex можно разложить в ряд, кот. сходится для любого Х. Поэтому eλ = 
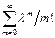= 1+ λ + λ2/2! + …+ λm/m! +… Тогда 
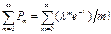= e—λ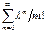 
= e—λ eλ =1. Найдем мат. ожидание и дисперсию СВ Х, распределенной по закону Пуассона. M(X) = 
= 
= 
= λ e—λ 
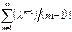= λe—λ eλ = λ = np. Суммирование начинается с m=1, т.к. 1-ый член суммы соответствующий m=0 равен 0. Дисперсию СВ Х найдем по формуле D(X) = M(X2) – (M(X))2. M(X2) = 
= e—λ 
= e—λ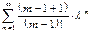 
= λ2 e—λ 
+ λ e—λ 
= λ2 e—λ eλ + λ e—λ eλ = λ2 +λ. Тогда D(X) = λ2 +λ — λ2 = λ = np. Т.о. мат. ожидание и дисперсия СВ, распределенной по закону Пуассона, совпадают и равны параметру этого распределения λ.
