Вычисление вер. попадания СВ, подчиненной нормальн. закону, в задан. интервал. Правило «трех сигм».
Для вычисления вероятности попадания СВ, распределенной нормально в задан. интервал (α;β) можно воспользоваться функцией Лапласа: Φ(х) = Определим далее, какой следует взять интервал с ценром в точке x=m, чтобы почти все значения СВ принадлежали ему. Для этого рассмотрим последовательно интервалы:
38. Понятие закона больших чисел. Содержание закона больших чисел в широком смысле: при очень большом числе случайных явлений средний их рез-т практически перестает быть случайным и может быть предсказан с большой степенью определенности. В узком смысле слова под законом больших чисел в теории вероятностей понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа опытов к некоторым определенным постоянным. Простейшей из этих теорем является теорема Бернулли. Она утверждает, что при большом числе опытов частота события приближается (точнее – сходится по вероятности) к вероятности этого события. Другие, более общие формулировки, устанавливабт факт и условия сходимости по вероятности тех или иных СВ к постоянным, не случайным величинам. Закон больших чисел играет важную роль в практических применениях теории вероятности. Св-во случайных величин при определенных условиях вести себя практически как не случайные позволяет уверенно оперировать с этими величинами, предсказывать рез-ты массовых случайных явлений (это большое число выполняемых однородных опытов или большое число складывающихся случайных воздействий, порождающих в своей совокупности случайную величину, подчиненную вполне определенному закону) почти с полной опреленностью.
|

 . Геометрически функция Лапласа представляет собой площадь под стандартной нормальной кривой на отрезке [-x; x]. Теор.: Функция распределения СВ Х, распределенной по нормальн. закону выражается через функцию Лапласа по формуле: F(x) = ½ + ½ Φ((x – a)/σ). Доказ-во: Используя формулу связи между функцией распределения и функцией плотности распределения, имеем: F(x) =
. Геометрически функция Лапласа представляет собой площадь под стандартной нормальной кривой на отрезке [-x; x]. Теор.: Функция распределения СВ Х, распределенной по нормальн. закону выражается через функцию Лапласа по формуле: F(x) = ½ + ½ Φ((x – a)/σ). Доказ-во: Используя формулу связи между функцией распределения и функцией плотности распределения, имеем: F(x) = 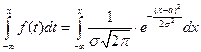 . Сделаем замену: t = (x – a)/σ; x = tσ+a; dx = σdt. Если х→ - ∞, то t→ - ∞; если t→x, то t→(x – a)/σ. Получаем
. Сделаем замену: t = (x – a)/σ; x = tσ+a; dx = σdt. Если х→ - ∞, то t→ - ∞; если t→x, то t→(x – a)/σ. Получаем  =
= 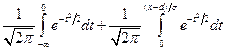 .
. 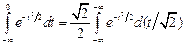 =
=  .
.  = ½ Φ((x – a)/σ). Значит F(x) =
= ½ Φ((x – a)/σ). Значит F(x) = 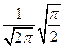 + ½ Φ((x – a)/σ) = ½ + ½ Φ((x – a)/σ). Геометрически функция распределения представляет собой площадь под нормальной кривой на интервале (- ∞; х).
+ ½ Φ((x – a)/σ) = ½ + ½ Φ((x – a)/σ). Геометрически функция распределения представляет собой площадь под нормальной кривой на интервале (- ∞; х). и т.д. Получим:
и т.д. Получим:  ;
;  ;
; 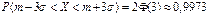 ;
;  . Как видно из вычислений, интервалом практически возможных значений СВ будет интервал
. Как видно из вычислений, интервалом практически возможных значений СВ будет интервал 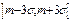 , т.к. последующ. вероятности увеличиваются незначительно. Это означает, что вер. того, что абсолютн. величина отклонений превысит утроенное среднее квадратическ. отклонение, очень мала. Т.о., зная среднее квадратич. отклонение и мат. ожидание СВ, ориентировочно можно указать интервал ее практически возможных значений. Это правило называется правилом трех сигм.
, т.к. последующ. вероятности увеличиваются незначительно. Это означает, что вер. того, что абсолютн. величина отклонений превысит утроенное среднее квадратическ. отклонение, очень мала. Т.о., зная среднее квадратич. отклонение и мат. ожидание СВ, ориентировочно можно указать интервал ее практически возможных значений. Это правило называется правилом трех сигм.


