При суммировании достаточно большого числа СВ закон распределении суммы неограниченно приближается к нормальному при соблюдении некоторых условий. Эти условия, которые математически можно сформулировать различным образом – в более или менее общем виде, - по существу сводятся к требованию, чтобы влияние на сумму отдельных слагаемых было равномерно малым, т.е. чтобы в состав суммы не входили члены, явно преобладающие над совокупностью остальных по своему влиянию на рассеивание суммы. Различные формы центральной предельной теоремы различаются между собой теми условиями, для кот. устанавливается это предельное св-во суммы СВ. В центральной предельной теореме рассматриваются законы распределения случайных величин. Согласно центральной предельной теореме, закон распределения суммы достаточно большого числа независимых (или слабо зависимых) слагаемых, каждое из которых в отдельности сравнительно мало влияет на сумму, сколь угодно близко к нормальному. В практических задачах центральную предельную теорему часто используют для вычисления вероятности того, что сумма нескольких СВ окажется в заданных пределах. Пусть Х1, Х2, …, Хn – независимые СВ с математическими ожиданиями m1, m2, …,mn и дисперсиями D1, D2, …, Dn. Предположим, что условия центральной предельной теоремы выполнены (величины Х1, Х2, …, Хn сравнимы по порядку своего влияния на рассеивание суммы) и число слагаемых n достаточно для того, чтобы закон распределения величины 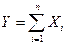 можно было считать приближенно нормальным. Тогда вероятность того, что СВ Y попадает в пределы участка (α, β), выражается формулой P(α <Y<β)=
можно было считать приближенно нормальным. Тогда вероятность того, что СВ Y попадает в пределы участка (α, β), выражается формулой P(α <Y<β)= 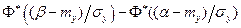 - формула (1), где my, σy – математическое ожидание и среднее квадратическое отклонение величины Y, Φ* – нормальная функция распределения.
- формула (1), где my, σy – математическое ожидание и среднее квадратическое отклонение величины Y, Φ* – нормальная функция распределения.
Заметим, что центральная предельная теорема может применяться не только к непрерывным, но и к дискретным СВ при условии, что мы будем оперировать не плотностями, а функциями распределения. Действительно, если величины Х1, Х2, …, Хn дискретны, то их сумма Х – также дискретная СВ и поэтому, строго говоря не может подчиняться нормальному закону. Однако все формулы типа формулы (1) остаются в силе, так как в них фигурируют не плотности, а функции распределения Частным случаем центральной предельной теоремы для ДСВ является теорема Лапласа.

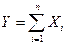 можно было считать приближенно нормальным. Тогда вероятность того, что СВ Y попадает в пределы участка (α, β), выражается формулой P(α <Y<β)=
можно было считать приближенно нормальным. Тогда вероятность того, что СВ Y попадает в пределы участка (α, β), выражается формулой P(α <Y<β)= 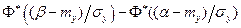 - формула (1), где my, σy – математическое ожидание и среднее квадратическое отклонение величины Y, Φ* – нормальная функция распределения.
- формула (1), где my, σy – математическое ожидание и среднее квадратическое отклонение величины Y, Φ* – нормальная функция распределения.


