Пусть случайный эксперимент описывается СВ Х. Повторяя случ. эксперимент n раз, получим последовательность наблюденных значений x1, x2, …, xn СВ Х, называемых выборкой из генеральной совокупности Ωx, описываемой функцией распределения F(x). Опред.: Выборочным средним наблюденных значений выборки назыв. величина, определяемая по формуле 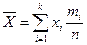 , где xi – наблюденное значение с частотой mi, n – число наблюдений,
, где xi – наблюденное значение с частотой mi, n – число наблюдений, 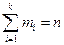 . Частоты mi могут быть равны 1, i =
. Частоты mi могут быть равны 1, i = 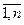 , тогда k=n. Опред.: Статистической дисперсией
, тогда k=n. Опред.: Статистической дисперсией 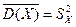 выборочного распределения назыв. среднее арифметическое квадратов отклонений значений наблюдений от средней арифметической
выборочного распределения назыв. среднее арифметическое квадратов отклонений значений наблюдений от средней арифметической  , т.е.
, т.е. 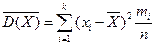 , где xi – наблюденное значение с частотой mi',
, где xi – наблюденное значение с частотой mi', 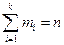 , n – число наблюдений. В кач-ве числовой хар-ки выборки так же применяется медиана. Чтобы вычислить ее все наблюдения располагают в порядке возрастания или убывания. При этом, если число вариант нечетно, т.е. 2m+1, то медианой является m+1 варианта (
, n – число наблюдений. В кач-ве числовой хар-ки выборки так же применяется медиана. Чтобы вычислить ее все наблюдения располагают в порядке возрастания или убывания. При этом, если число вариант нечетно, т.е. 2m+1, то медианой является m+1 варианта (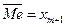 ); если же число вариант четное, то медиана равна среднему арифметическому двух средних значений:
); если же число вариант четное, то медиана равна среднему арифметическому двух средних значений: 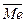 = (xm+xm+1)/2. Хар-ка ассиметрии выборочного распределения вычисляется по формуле
= (xm+xm+1)/2. Хар-ка ассиметрии выборочного распределения вычисляется по формуле 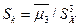 , а эксцесс выборочного распределения определяется характеристикой
, а эксцесс выборочного распределения определяется характеристикой 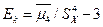 . Обобщающими хар-ками выборочных распределений являются статистич. моменты распределения. Начальные статистич. моменты k-того порядка:
. Обобщающими хар-ками выборочных распределений являются статистич. моменты распределения. Начальные статистич. моменты k-того порядка: 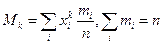 . Тогда: при k =0 M0 =
. Тогда: при k =0 M0 = 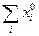 (mi/n) = 1; при k =1 M1 =
(mi/n) = 1; при k =1 M1 = 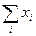 (mi/n) =
(mi/n) =  ; при k =2 M2 =
; при k =2 M2 = 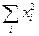 (mi/n) =
(mi/n) =  2; при k =3 M3 =
2; при k =3 M3 = 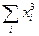 (mi/n) =
(mi/n) =  3; при k =4 M4 =
3; при k =4 M4 = 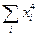 (mi/n) =
(mi/n) =  4 и т.д. Практически используются моменты первых четырех порядков. Центральные статистич. моменты k-того порядка:
4 и т.д. Практически используются моменты первых четырех порядков. Центральные статистич. моменты k-того порядка: 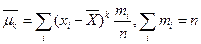 . Тогда: при k =0
. Тогда: при k =0 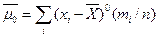 =1; при k =1
=1; при k =1 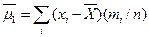 =0; при k =2
=0; при k =2 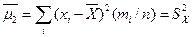 - статистич. дисперсия; при k =3
- статистич. дисперсия; при k =3 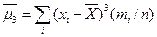 ; при k =4
; при k =4 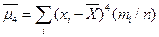 и т.д. Отметим, что центральный статистич. момент 3-его порядка служит мерой ассиметрии распределения выборки. Если распределение симметрично, то
и т.д. Отметим, что центральный статистич. момент 3-его порядка служит мерой ассиметрии распределения выборки. Если распределение симметрично, то 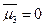 . На практике моменты порядка выше четвертого почти не применяются, т.к. обладают очень высокой дисперсией и их сколько-нибудь надежное определение потребовало бы выборок большого объема.
. На практике моменты порядка выше четвертого почти не применяются, т.к. обладают очень высокой дисперсией и их сколько-нибудь надежное определение потребовало бы выборок большого объема.

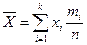 , где xi – наблюденное значение с частотой mi, n – число наблюдений,
, где xi – наблюденное значение с частотой mi, n – число наблюдений, 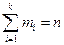 . Частоты mi могут быть равны 1, i =
. Частоты mi могут быть равны 1, i = 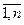 , тогда k=n. Опред.: Статистической дисперсией
, тогда k=n. Опред.: Статистической дисперсией 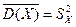 выборочного распределения назыв. среднее арифметическое квадратов отклонений значений наблюдений от средней арифметической
выборочного распределения назыв. среднее арифметическое квадратов отклонений значений наблюдений от средней арифметической  , т.е.
, т.е. 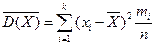 , где xi – наблюденное значение с частотой mi',
, где xi – наблюденное значение с частотой mi', 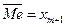 ); если же число вариант четное, то медиана равна среднему арифметическому двух средних значений:
); если же число вариант четное, то медиана равна среднему арифметическому двух средних значений: 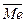 = (xm+xm+1)/2. Хар-ка ассиметрии выборочного распределения вычисляется по формуле
= (xm+xm+1)/2. Хар-ка ассиметрии выборочного распределения вычисляется по формуле 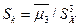 , а эксцесс выборочного распределения определяется характеристикой
, а эксцесс выборочного распределения определяется характеристикой 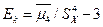 . Обобщающими хар-ками выборочных распределений являются статистич. моменты распределения. Начальные статистич. моменты k-того порядка:
. Обобщающими хар-ками выборочных распределений являются статистич. моменты распределения. Начальные статистич. моменты k-того порядка: 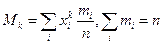 . Тогда: при k =0 M0 =
. Тогда: при k =0 M0 = 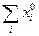 (mi/n) = 1; при k =1 M1 =
(mi/n) = 1; при k =1 M1 = 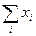 (mi/n) =
(mi/n) = 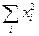 (mi/n) =
(mi/n) = 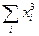 (mi/n) =
(mi/n) = 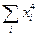 (mi/n) =
(mi/n) = 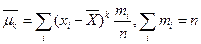 . Тогда: при k =0
. Тогда: при k =0 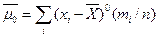 =1; при k =1
=1; при k =1 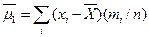 =0; при k =2
=0; при k =2 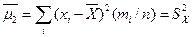 - статистич. дисперсия; при k =3
- статистич. дисперсия; при k =3 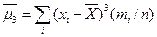 ; при k =4
; при k =4 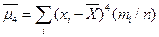 и т.д. Отметим, что центральный статистич. момент 3-его порядка служит мерой ассиметрии распределения выборки. Если распределение симметрично, то
и т.д. Отметим, что центральный статистич. момент 3-его порядка служит мерой ассиметрии распределения выборки. Если распределение симметрично, то 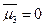 . На практике моменты порядка выше четвертого почти не применяются, т.к. обладают очень высокой дисперсией и их сколько-нибудь надежное определение потребовало бы выборок большого объема.
. На практике моменты порядка выше четвертого почти не применяются, т.к. обладают очень высокой дисперсией и их сколько-нибудь надежное определение потребовало бы выборок большого объема.


