Пусть задана СВ Х с неизвестным мат. ожиданием М(Х) и дисперсией D(X). Покажем, что оценкой для дисперсии D(X) СВ Х служит ее статистическая дисперсия 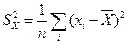 - формула (1). Т.к. значения центральных статистических моментов не зависят от выбора начала отсчета величины (новый отсчет отличается от старого на постоянную величину), то формулу (1) можно записать:
- формула (1). Т.к. значения центральных статистических моментов не зависят от выбора начала отсчета величины (новый отсчет отличается от старого на постоянную величину), то формулу (1) можно записать: 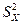 =
= 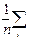 (xi – M(X) +M(X) —
(xi – M(X) +M(X) —  )2 =
)2 = 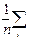 ((xi – M(X)) – (
((xi – M(X)) – ( - M(X)))2 =
- M(X)))2 = 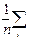 ((xi – M(X))2 – 2(xi – M(X))(
((xi – M(X))2 – 2(xi – M(X))( - M(X)) + (
- M(X)) + ( - M(X))2) =
- M(X))2) = 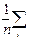 ((xi – M(X))2 – 2(
((xi – M(X))2 – 2( - M(X))(
- M(X))(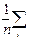 xi – M(X)) + (
xi – M(X)) + ( - M(X))2 =
- M(X))2 = 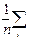 ((xi – M(X))2 – 2(
((xi – M(X))2 – 2( - M(X))2 + (
- M(X))2 + ( - M(X))2 =
- M(X))2 = 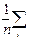 ((xi – M(X))2 – (
((xi – M(X))2 – ( - M(X))2. Рассматривая xi, i =
- M(X))2. Рассматривая xi, i = 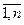 , как независимые СВ Х1, Х2, …, Хn с тем же законом распределения, что и величина Х, будем иметь: M(
, как независимые СВ Х1, Х2, …, Хn с тем же законом распределения, что и величина Х, будем иметь: M(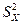 ) = M(
) = M(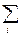 (xi – M(X))2
(xi – M(X))2 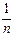 - (
- ( - M(X))2) =
- M(X))2) = 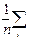 M(xi – M(X))2 - M(
M(xi – M(X))2 - M( - M(X))2 =
- M(X))2 = 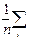 M(Xi – M(X))2 - D(
M(Xi – M(X))2 - D( ) =
) = 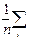 D(Xi) -
D(Xi) - 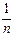 D(X) = D(X) -
D(X) = D(X) - 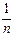 D(X) = (—(n – 1)/n)D(X). Как видно из полученного рез-та, статистич. дисперсия не является несмещенной оценкой, т.к. отличается от D(X) на величину D(X)/n. Для получения несмещенной оценки умножим статистич. дисперсию на n/(n – 1) и получим статистич. дисперсию
D(X) = (—(n – 1)/n)D(X). Как видно из полученного рез-та, статистич. дисперсия не является несмещенной оценкой, т.к. отличается от D(X) на величину D(X)/n. Для получения несмещенной оценки умножим статистич. дисперсию на n/(n – 1) и получим статистич. дисперсию 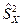 = (n/(n – 1))
= (n/(n – 1)) 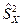 = (- 1/(n – 1))
= (- 1/(n – 1)) 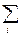 (xi –
(xi –  )2, которая и будет несмещенной оценкой дисперсии СВ Х, так как M(
)2, которая и будет несмещенной оценкой дисперсии СВ Х, так как M(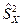 ) = D(X). Рассмотрим рав-во
) = D(X). Рассмотрим рав-во 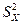 =
= 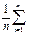 (xi – M(X))2 – (
(xi – M(X))2 – ( - M(X))2 и покажем, что оценка
- M(X))2 и покажем, что оценка 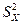 состоятельна. Слагаемое
состоятельна. Слагаемое 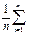 (xi – M(X))2 приведенной выше формулы является средним арифметическим n независимых, одинаково распределенных величин (xi – M(X))2. Согласно закону больших чисел,
(xi – M(X))2 приведенной выше формулы является средним арифметическим n независимых, одинаково распределенных величин (xi – M(X))2. Согласно закону больших чисел, 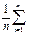 (xi – M(X))2
(xi – M(X))2 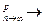 M(xi – M(X))2 = D(X). Второе слагаемое (
M(xi – M(X))2 = D(X). Второе слагаемое ( - M(X))2 в силу закона больших чисел сходится по вероятности к нулю:
- M(X))2 в силу закона больших чисел сходится по вероятности к нулю: 
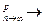 M(X). В самом деле, если P((
M(X). В самом деле, если P(( - M(X))2 > ε)→0 при n→∞, то и P(|
- M(X))2 > ε)→0 при n→∞, то и P(|  - M(X)|>
- M(X)|> 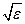 )→0 при n→∞. Т.к. статистич. дисперсия является суммой двух слагаемых, одно из которых сходится по вероятности к D(X), а другое – к нулю, то
)→0 при n→∞. Т.к. статистич. дисперсия является суммой двух слагаемых, одно из которых сходится по вероятности к D(X), а другое – к нулю, то 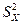
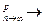 D(X), что свидетельствует о состоятельности оценки
D(X), что свидетельствует о состоятельности оценки 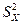 .
.