Критерий согласия Пирсона основан на выборе определенной меры расхождения между теоретическим и эмпирическим (полученным из эксперимента) распределениями. Причем задачу проверки согласованности теории с опытными данными можно сформулировать в следующем виде: имеется выборка х1, х2, …, хn наблюденных значений некоторой СВ Х. Требуется определить, что выборочное распределение принадлежит определенному распределению (нормальному, биномиальному, показательному и т.д.) – гипотеза Н0 против альтернативной гипотезы Н1 – распределение не принадлежит выбранному распределению. Допустим вначале, что гипотеза Н0 полностью определяет вид функции Р, и вероятность P(xj 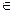 Si) может быть вычислена для любого заданного мн-ва S1, S2, …, Sk – это либо интервалы для непрерывной СВ, либо группы отдельных значений дискретной СВ, не имеющие общих точек. Пусть pi = P(xj
Si) может быть вычислена для любого заданного мн-ва S1, S2, …, Sk – это либо интервалы для непрерывной СВ, либо группы отдельных значений дискретной СВ, не имеющие общих точек. Пусть pi = P(xj 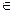 Si) – вероятность того, что СВ Х принимает значения, принадлежащие мн-ву Si и
Si) – вероятность того, что СВ Х принимает значения, принадлежащие мн-ву Si и  =1, причем все pi>0, i =
=1, причем все pi>0, i = 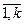 . Соответствующие групповые частоты в выборке m1, m2, …, mk, т.е. mi – это число значений СВ Х из выборки, попавших в Si. Ясно, что
. Соответствующие групповые частоты в выборке m1, m2, …, mk, т.е. mi – это число значений СВ Х из выборки, попавших в Si. Ясно, что 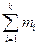 =n. Если проверяемая гипотеза Н0 верна, то распределение выборки можно рассматривать как статистический аналог для генерального распределения, определяемого функцией р(х). Это значит, что mi представляет собой частоту появления события с вероятностью pi = P(Si) в нашей последовательности из n наблюдений. Следовательно, любое мн-во Si имеет в первом распределении относительные частоты mi/n, а во втором – вероятности pi. Тогда, согласно методу наименьших квадратов, за меру расхождения между распределением выборки и теоретическим распределением примем величину
=n. Если проверяемая гипотеза Н0 верна, то распределение выборки можно рассматривать как статистический аналог для генерального распределения, определяемого функцией р(х). Это значит, что mi представляет собой частоту появления события с вероятностью pi = P(Si) в нашей последовательности из n наблюдений. Следовательно, любое мн-во Si имеет в первом распределении относительные частоты mi/n, а во втором – вероятности pi. Тогда, согласно методу наименьших квадратов, за меру расхождения между распределением выборки и теоретическим распределением примем величину 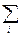 Ci(mi/n - pi)2, где Ci – произвольный коэффициент. Пирсон доказал, что если Ci = n/ pi, то получится мера расхождения вида χ2 =
Ci(mi/n - pi)2, где Ci – произвольный коэффициент. Пирсон доказал, что если Ci = n/ pi, то получится мера расхождения вида χ2 =  , такая, что при увеличении объема выборки выборочное рапределение величины χ2 стремится к предельному распределению χ2 с υ = κ – r – 1 степенями свободы (к – число интервалов или групп, на кторые разбито все мн-во наблюденных данных, r – число параметров гипотетического распределения вероятностей Р, оцениваемых по данным выборки). Это утверждение следует из того, что если гипотеза Н0 верна, то совместным распределением групповых частот mi, i =
, такая, что при увеличении объема выборки выборочное рапределение величины χ2 стремится к предельному распределению χ2 с υ = κ – r – 1 степенями свободы (к – число интервалов или групп, на кторые разбито все мн-во наблюденных данных, r – число параметров гипотетического распределения вероятностей Р, оцениваемых по данным выборки). Это утверждение следует из того, что если гипотеза Н0 верна, то совместным распределением групповых частот mi, i = 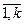 , является простое обощение биномиального распределения, и тогда случайные величины Xi = (mi - npi)/
, является простое обощение биномиального распределения, и тогда случайные величины Xi = (mi - npi)/ 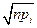 нормально распределены, а их сумма квадратов χ2 =
нормально распределены, а их сумма квадратов χ2 = 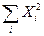 имеет распределение χ2 с υ = κ – r – 1 степенями свободы. Для того, чтобы величина критерия приближенно имела χ2-распределение, теоретические частоты npi должны быть не слишком малыми.
имеет распределение χ2 с υ = κ – r – 1 степенями свободы. Для того, чтобы величина критерия приближенно имела χ2-распределение, теоретические частоты npi должны быть не слишком малыми.

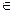 Si) может быть вычислена для любого заданного мн-ва S1, S2, …, Sk – это либо интервалы для непрерывной СВ, либо группы отдельных значений дискретной СВ, не имеющие общих точек. Пусть pi = P(xj
Si) может быть вычислена для любого заданного мн-ва S1, S2, …, Sk – это либо интервалы для непрерывной СВ, либо группы отдельных значений дискретной СВ, не имеющие общих точек. Пусть pi = P(xj  =1, причем все pi>0, i =
=1, причем все pi>0, i = 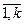 . Соответствующие групповые частоты в выборке m1, m2, …, mk, т.е. mi – это число значений СВ Х из выборки, попавших в Si. Ясно, что
. Соответствующие групповые частоты в выборке m1, m2, …, mk, т.е. mi – это число значений СВ Х из выборки, попавших в Si. Ясно, что 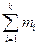 =n. Если проверяемая гипотеза Н0 верна, то распределение выборки можно рассматривать как статистический аналог для генерального распределения, определяемого функцией р(х). Это значит, что mi представляет собой частоту появления события с вероятностью pi = P(Si) в нашей последовательности из n наблюдений. Следовательно, любое мн-во Si имеет в первом распределении относительные частоты mi/n, а во втором – вероятности pi. Тогда, согласно методу наименьших квадратов, за меру расхождения между распределением выборки и теоретическим распределением примем величину
=n. Если проверяемая гипотеза Н0 верна, то распределение выборки можно рассматривать как статистический аналог для генерального распределения, определяемого функцией р(х). Это значит, что mi представляет собой частоту появления события с вероятностью pi = P(Si) в нашей последовательности из n наблюдений. Следовательно, любое мн-во Si имеет в первом распределении относительные частоты mi/n, а во втором – вероятности pi. Тогда, согласно методу наименьших квадратов, за меру расхождения между распределением выборки и теоретическим распределением примем величину 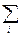 Ci(mi/n - pi)2, где Ci – произвольный коэффициент. Пирсон доказал, что если Ci = n/ pi, то получится мера расхождения вида χ2 =
Ci(mi/n - pi)2, где Ci – произвольный коэффициент. Пирсон доказал, что если Ci = n/ pi, то получится мера расхождения вида χ2 =  , такая, что при увеличении объема выборки выборочное рапределение величины χ2 стремится к предельному распределению χ2 с υ = κ – r – 1 степенями свободы (к – число интервалов или групп, на кторые разбито все мн-во наблюденных данных, r – число параметров гипотетического распределения вероятностей Р, оцениваемых по данным выборки). Это утверждение следует из того, что если гипотеза Н0 верна, то совместным распределением групповых частот mi, i =
, такая, что при увеличении объема выборки выборочное рапределение величины χ2 стремится к предельному распределению χ2 с υ = κ – r – 1 степенями свободы (к – число интервалов или групп, на кторые разбито все мн-во наблюденных данных, r – число параметров гипотетического распределения вероятностей Р, оцениваемых по данным выборки). Это утверждение следует из того, что если гипотеза Н0 верна, то совместным распределением групповых частот mi, i = 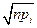 нормально распределены, а их сумма квадратов χ2 =
нормально распределены, а их сумма квадратов χ2 = 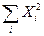 имеет распределение χ2 с υ = κ – r – 1 степенями свободы. Для того, чтобы величина критерия приближенно имела χ2-распределение, теоретические частоты npi должны быть не слишком малыми.
имеет распределение χ2 с υ = κ – r – 1 степенями свободы. Для того, чтобы величина критерия приближенно имела χ2-распределение, теоретические частоты npi должны быть не слишком малыми.


