Уровень значимости и мощность критерия. Ошибки первого и второго рода.

Проверяя гипотезы с помощью статистического критерия, может возникнуть одна из четырех ситуаций: 1) гипотеза H₀ истинна (и поэтому H₁ – ложна) и предпринимается действие А; 2) гипотеза H₁ истинна (и поэтому H₀ – ложна) и предпринимается действие А; 3)) гипотеза H₀ истинна (и поэтому H₁ – ложна) и предпринимается действие В; 4) гипотеза H₁ истинна (и поэтому H₀ – ложна) и предпринимается действие В. В ситуациях 2 и 3 получается ошибка. Существует 2 типа ошибок. Ошибка, состоящая в принятии гипотезы H₀, когда она ложна (ошибка второго рода), качественно отличается от ошибки, состоящей в отвержении H₀, когда она истинна (ошибка первого рода). При этом числа α_i = α_i(δ) = P_i(δ(X)≠ H_i), характеризующие вероятность отвержения гипотезы H_i, когда она верна, называют вероятностями ошибок (i+1)-го рода критерия δ. Набором вероятностей α_i(δ) ошибочных решений характеризуется кач-вом критерия δ. Правильное решение также может быть принято двумя способами (ситуации 1 и 4): когда гипотеза H₀ принимается, ибо она верна, и когда гипотеза H₀ отвергается, ибо она ложна. В ситуации 1 не совершается ошибка первого рода, в ситуации 4 – второго рода.

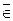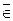Уровень значимости критерия не меняет степени риска, связанного с возможностью ошибки второго рода, т.е. с принятием неверной гипотезы. И при данном уровне значимости можно по-разному определить критическую область. Как правило, ее определяют так, чтобы мощность критерия 1 – α₁(δ) была возможно большей: P (X ] x₁; x₂[|H₁) = max. Мощностью критерия δ называется вероятность 1 – α₁(δ) несовершения ошибки второго рода. Чем больше мощность критерия, тем меньше вероятность принятия неверной гипотезы.