Пусть х0 – любое действительное число (точка на числовой прямой). Окрестностью точки х0 называется любой интервал(a;b),содержащий точку х0. В частности,интервал(х0-ɛ,х0+ɛ),где ɛ>0, называется ɛ-окрестностью точки х0. Число х0 называется центром, а число ɛ-радиусом.Если х Є (х0-ɛ;х0+ɛ),то выполняется неравенство х0-ɛ<х<х0+ɛ, или, что то же,|x-x0|<ɛ. Выполнение последнего неравенства означает попадание точки x в ɛ-окрестность точки х0.Число b называется пределом функции y=f(x) при х -->a,если для любой окрестности B(b) точки b найдётся такая проколотая окрестность B̂(a) точки a,что как только хЄ В̂(a), то f(х)Є В(b), что обозначается b=limf(x) или f(x)-->b при x-->a(f(x) стремится к b при х, стремящегося к а)b=limf(x) ó  B(b)
B(b) 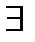 B̂(a) (xЄB̂(a) =>f(x) Є B(b)) на языке «ɛ», «δ» (
B̂(a) (xЄB̂(a) =>f(x) Є B(b)) на языке «ɛ», «δ» ( ɛ> 0 Ǝδ>0
ɛ> 0 Ǝδ>0  x: |x-x0| <δ,x≠x0 => |f(x)-A|<ɛ) ólimf(x)=A. Предел последовательности:если члены одной последовательности являются членами другой последовательности,то 1 по отношению ко 2 называется последовательностью.Теорема:А)лемо о выборе: из всякого ограниченного числового множества можно выбрать сходящуюся подпоследовательность.Б) об ограниченной монотонной последовательности: Ограниченная монотонная последовательность сходится в частности огран. сверху неубыв. послед. сходится точно так же как и огран. снизу невозрастающая.
x: |x-x0| <δ,x≠x0 => |f(x)-A|<ɛ) ólimf(x)=A. Предел последовательности:если члены одной последовательности являются членами другой последовательности,то 1 по отношению ко 2 называется последовательностью.Теорема:А)лемо о выборе: из всякого ограниченного числового множества можно выбрать сходящуюся подпоследовательность.Б) об ограниченной монотонной последовательности: Ограниченная монотонная последовательность сходится в частности огран. сверху неубыв. послед. сходится точно так же как и огран. снизу невозрастающая.

 B(b)
B(b) 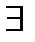 B̂(a) (xЄB̂(a) =>f(x) Є B(b)) на языке «ɛ», «δ» (
B̂(a) (xЄB̂(a) =>f(x) Є B(b)) на языке «ɛ», «δ» ( ɛ> 0 Ǝδ>0
ɛ> 0 Ǝδ>0  x: |x-x0| <δ,x≠x0 => |f(x)-A|<ɛ) ólimf(x)=A. Предел последовательности:если члены одной последовательности являются членами другой последовательности,то 1 по отношению ко 2 называется последовательностью.Теорема:А)лемо о выборе: из всякого ограниченного числового множества можно выбрать сходящуюся подпоследовательность.Б) об ограниченной монотонной последовательности: Ограниченная монотонная последовательность сходится в частности огран. сверху неубыв. послед. сходится точно так же как и огран. снизу невозрастающая.
x: |x-x0| <δ,x≠x0 => |f(x)-A|<ɛ) ólimf(x)=A. Предел последовательности:если члены одной последовательности являются членами другой последовательности,то 1 по отношению ко 2 называется последовательностью.Теорема:А)лемо о выборе: из всякого ограниченного числового множества можно выбрать сходящуюся подпоследовательность.Б) об ограниченной монотонной последовательности: Ограниченная монотонная последовательность сходится в частности огран. сверху неубыв. послед. сходится точно так же как и огран. снизу невозрастающая.


