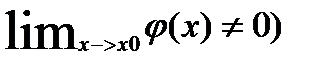Бесконечно малые и бесконечно большие функции:Функция у=f(x) называется бесконечно малой при xàx0, если  =0Функция у=f(x) называется бесконечно большой при xàx0, если для любого числа М>0 существует число δ=δ(М)>0,что для всех х,удовлетворяющих неравенству 0<|х-х0|<δ,выполняется неравенство |f(x)|>M.Записывают
=0Функция у=f(x) называется бесконечно большой при xàx0, если для любого числа М>0 существует число δ=δ(М)>0,что для всех х,удовлетворяющих неравенству 0<|х-х0|<δ,выполняется неравенство |f(x)|>M.Записывают  или f(x)->∞ при x->x0. Коротко: (
или f(x)->∞ при x->x0. Коротко: ( M>0
M>0 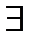 δ>0
δ>0  x: |x-x0|<δ, x≠x0=>|f(x)>M)ó
x: |x-x0|<δ, x≠x0=>|f(x)>M)ó 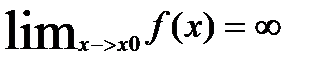 Теоремы:1)Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция. Следствие: Так как всякая б.м.ф. ограничена, то из теоремы (2) вытекает: произведение двух б.м.ф.есть функция бесконечно малая.
Теоремы:1)Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция. Следствие: Так как всякая б.м.ф. ограничена, то из теоремы (2) вытекает: произведение двух б.м.ф.есть функция бесконечно малая.
2)Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая. Следствие: Произведение б.м.ф. на число есть функция бесконечно малая.3)Частное от деления б.м.ф. на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.4) Если функция α(х) – бесконечно малая (α≠0), то функция 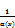 есть б.б.ф. и наоборот: если функция f(x)- б.б.,то
есть б.б.ф. и наоборот: если функция f(x)- б.б.,то 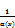 –б.м. Примеры:1)Пусть
–б.м. Примеры:1)Пусть  =0,
=0,  ≠0.Функция
≠0.Функция  может быть представлена в виде произведение б.м.ф. α(х) на ограниченную функцию
может быть представлена в виде произведение б.м.ф. α(х) на ограниченную функцию  . Но тогда из теоремы (2) вытекает, что частное
. Но тогда из теоремы (2) вытекает, что частное  =α(x)*
=α(x)*  есть функция бесконечно малая.2)Пусть α(x) есть б.м.ф. при хàx0, т.е.
есть функция бесконечно малая.2)Пусть α(x) есть б.м.ф. при хàx0, т.е. 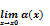 =0. Тогда (
=0. Тогда ( ε>0
ε>0  δ>0
δ>0  x: 0<|x-x0|<δ)=> |α(x)|<ε, т.е.
x: 0<|x-x0|<δ)=> |α(x)|<ε, т.е.  >
>  , т.е.
, т.е.  >М, где М=
>М, где М=  . А это означает, что функция
. А это означает, что функция 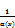 есть бесконечно большая. Аналогично доказывается обратное утверждение.3)функция
есть бесконечно большая. Аналогично доказывается обратное утверждение.3)функция 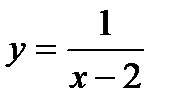 есть б.б.ф. при x->2.Основные теоремы о пределах:1) Предел суммы (разности) двух функций равен сумме (разности) их пределов:
есть б.б.ф. при x->2.Основные теоремы о пределах:1) Предел суммы (разности) двух функций равен сумме (разности) их пределов:  2)Предел произведения двух функций равен произведению их пределов
2)Предел произведения двух функций равен произведению их пределов 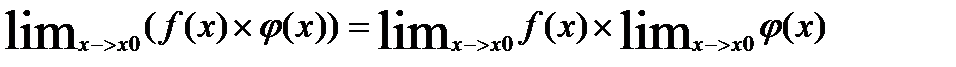
3) Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю: 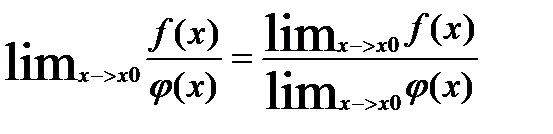 (
(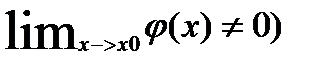

 =0Функция у=f(x) называется бесконечно большой при xàx0, если для любого числа М>0 существует число δ=δ(М)>0,что для всех х,удовлетворяющих неравенству 0<|х-х0|<δ,выполняется неравенство |f(x)|>M.Записывают
=0Функция у=f(x) называется бесконечно большой при xàx0, если для любого числа М>0 существует число δ=δ(М)>0,что для всех х,удовлетворяющих неравенству 0<|х-х0|<δ,выполняется неравенство |f(x)|>M.Записывают  или f(x)->∞ при x->x0. Коротко: (
или f(x)->∞ при x->x0. Коротко: ( M>0
M>0 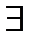 δ>0
δ>0  x: |x-x0|<δ, x≠x0=>|f(x)>M)ó
x: |x-x0|<δ, x≠x0=>|f(x)>M)ó 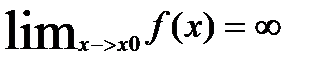 Теоремы:1)Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция. Следствие: Так как всякая б.м.ф. ограничена, то из теоремы (2) вытекает: произведение двух б.м.ф.есть функция бесконечно малая.
Теоремы:1)Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция. Следствие: Так как всякая б.м.ф. ограничена, то из теоремы (2) вытекает: произведение двух б.м.ф.есть функция бесконечно малая.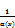 есть б.б.ф. и наоборот: если функция f(x)- б.б.,то
есть б.б.ф. и наоборот: если функция f(x)- б.б.,то  может быть представлена в виде произведение б.м.ф. α(х) на ограниченную функцию
может быть представлена в виде произведение б.м.ф. α(х) на ограниченную функцию  . Но тогда из теоремы (2) вытекает, что частное
. Но тогда из теоремы (2) вытекает, что частное 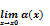 =0. Тогда (
=0. Тогда ( ε>0
ε>0  δ>0
δ>0  x: 0<|x-x0|<δ)=> |α(x)|<ε, т.е.
x: 0<|x-x0|<δ)=> |α(x)|<ε, т.е.  >
>  , т.е.
, т.е. 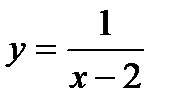 есть б.б.ф. при x->2.Основные теоремы о пределах:1) Предел суммы (разности) двух функций равен сумме (разности) их пределов:
есть б.б.ф. при x->2.Основные теоремы о пределах:1) Предел суммы (разности) двух функций равен сумме (разности) их пределов:  2)Предел произведения двух функций равен произведению их пределов
2)Предел произведения двух функций равен произведению их пределов 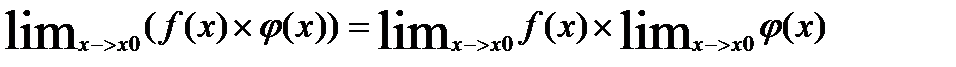
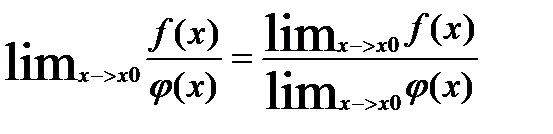 (
(