Сравнение бесконечно малых функций производится путем нахождения предела их отношения. Пусть α (x) и β (x) – бмф при x → a, причем  Тогда если: 1) А = 1, то α (x) и β (x) называются эквивалентными бмф при x → a, что записывается в виде α (x) ~ β (x); 2) A ≠ 0и A ≠∞, то α (x) и β (x) – бмф одного порядка малости при x → a; 3) A = 0, то β (x) есть бмф более высокого порядка малости, чем α (x), при x → a, что записывается в виде β (x) = o (α(x)); 4) A =∞, то α (x) есть бмф более высокого порядка малости, чем β (x), при x → a, что записывается в виде α (x) =o (β (x)). Свойства бесконечно малых функций 1. Алгебраическая сумма конечного числа бесконечно малых функций есть бмф. 2. Произведение бесконечно малой функции на ограниченную функцию есть бмф. 3. Если α (x) ~ β (x), то β (x) ~ α (x). 4. Если α (x) ~ β (x) и β (x) ~γ (x), то α (x) ~γ (x).5. Если α (x) ~ β (x), то α (x) − β (x) = o (α(x)) = o (β(x)).6. Если α (x) ~ α′ (x) и β (x) ~ β ′ (x), то
Тогда если: 1) А = 1, то α (x) и β (x) называются эквивалентными бмф при x → a, что записывается в виде α (x) ~ β (x); 2) A ≠ 0и A ≠∞, то α (x) и β (x) – бмф одного порядка малости при x → a; 3) A = 0, то β (x) есть бмф более высокого порядка малости, чем α (x), при x → a, что записывается в виде β (x) = o (α(x)); 4) A =∞, то α (x) есть бмф более высокого порядка малости, чем β (x), при x → a, что записывается в виде α (x) =o (β (x)). Свойства бесконечно малых функций 1. Алгебраическая сумма конечного числа бесконечно малых функций есть бмф. 2. Произведение бесконечно малой функции на ограниченную функцию есть бмф. 3. Если α (x) ~ β (x), то β (x) ~ α (x). 4. Если α (x) ~ β (x) и β (x) ~γ (x), то α (x) ~γ (x).5. Если α (x) ~ β (x), то α (x) − β (x) = o (α(x)) = o (β(x)).6. Если α (x) ~ α′ (x) и β (x) ~ β ′ (x), то 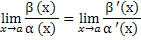 . Пример. Рассмотрим функции
. Пример. Рассмотрим функции  ,
, 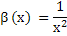 ,
, 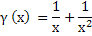
Тогда α (x)– бмф при x →∞, β (x)– бмф при x→∞, γ (x) – бмф при x→∞.Частное 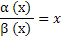 есть функция бесконечно большая при x→∞;Частное
есть функция бесконечно большая при x→∞;Частное 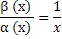 есть бмф при x→∞;Частное
есть бмф при x→∞;Частное 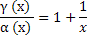 есть функция, имеющая конечный предел при x→∞.
есть функция, имеющая конечный предел при x→∞.

 Тогда если: 1) А = 1, то α (x) и β (x) называются эквивалентными бмф при x → a, что записывается в виде α (x) ~ β (x); 2) A ≠ 0и A ≠∞, то α (x) и β (x) – бмф одного порядка малости при x → a; 3) A = 0, то β (x) есть бмф более высокого порядка малости, чем α (x), при x → a, что записывается в виде β (x) = o (α(x)); 4) A =∞, то α (x) есть бмф более высокого порядка малости, чем β (x), при x → a, что записывается в виде α (x) =o (β (x)). Свойства бесконечно малых функций 1. Алгебраическая сумма конечного числа бесконечно малых функций есть бмф. 2. Произведение бесконечно малой функции на ограниченную функцию есть бмф. 3. Если α (x) ~ β (x), то β (x) ~ α (x). 4. Если α (x) ~ β (x) и β (x) ~γ (x), то α (x) ~γ (x).5. Если α (x) ~ β (x), то α (x) − β (x) = o (α(x)) = o (β(x)).6. Если α (x) ~ α′ (x) и β (x) ~ β ′ (x), то
Тогда если: 1) А = 1, то α (x) и β (x) называются эквивалентными бмф при x → a, что записывается в виде α (x) ~ β (x); 2) A ≠ 0и A ≠∞, то α (x) и β (x) – бмф одного порядка малости при x → a; 3) A = 0, то β (x) есть бмф более высокого порядка малости, чем α (x), при x → a, что записывается в виде β (x) = o (α(x)); 4) A =∞, то α (x) есть бмф более высокого порядка малости, чем β (x), при x → a, что записывается в виде α (x) =o (β (x)). Свойства бесконечно малых функций 1. Алгебраическая сумма конечного числа бесконечно малых функций есть бмф. 2. Произведение бесконечно малой функции на ограниченную функцию есть бмф. 3. Если α (x) ~ β (x), то β (x) ~ α (x). 4. Если α (x) ~ β (x) и β (x) ~γ (x), то α (x) ~γ (x).5. Если α (x) ~ β (x), то α (x) − β (x) = o (α(x)) = o (β(x)).6. Если α (x) ~ α′ (x) и β (x) ~ β ′ (x), то 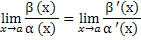 . Пример. Рассмотрим функции
. Пример. Рассмотрим функции  ,
, 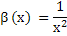 ,
, 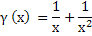
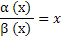 есть функция бесконечно большая при x→∞;Частное
есть функция бесконечно большая при x→∞;Частное 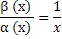 есть бмф при x→∞;Частное
есть бмф при x→∞;Частное 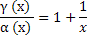 есть функция, имеющая конечный предел при x→∞.
есть функция, имеющая конечный предел при x→∞.


