Схема міжгалузевого балансу.
МАТЕМАТИЧНІ МОДЕЛІ В ЕКОНОМІЦІ Вступ Мета курсу – розглянути основні принципи побудови математичних моделей економічних процесів і специфічні, з математичної точки зору, методи їх дослідження. Для розуміння і засвоєння курсу необхідні знання з курсів математичного аналізу, лінійної алгебри, теорії диференціальних рівнянь, методів оптимізації - задачі лінійного і опуклого програмування, принцип максимуму Понтрягіна для задач оптимального керування. Курс складається з двох частин – моделі макроекономіки і моделі мікроекономіки. Макроекономіка – це розділ економічної науки, яка аналізує поведінку та розвиток економіки як єдиного цілого. При цьому вивчаються закономірності взаємодії сукупних величин та показників типу загального рівня цін та безробіття, загального попиту та інвестицій, загального попиту та пропозицій, їх вплив на зміну в обсязі виробництва і економічне зростання, тощо. Явища, що вивчає макроекономіка стосуються всіх членів суспільства. Розглянемо термін «математична економіка». Реальні економічні процеси, які протікають в сучасному промисловому виробництві, настільки складні і багатогранні, що для їх вивчення необхідно залучати цілий комплекс наук від політекономії до кібернетики. Математичне моделювання економічних явищ є потужним засобом досліджень. Водночас спектр застосування математичних методів є теж дуже широкий. Розгляд конкретних аспектів процесу планування народного господарства призводить до різноманітних засобів опису, які виражаються у виді систем рівнянь, нерівностей, співвідношень між параметрами, які характеризують досліджуваний економічний об’єкт. Математична економіка представляє собою методологічну основу, яка дозволяє знайти те спільне, що міститься в різних по формі і суті моделях конкретних об’єктів, вказати можливі якісні властивості розв’язків відповідних оптимізаційних задач, запропонувати методи їх дослідження. Схема міжгалузевого балансу. Статистична модель «витрати-випуск» або модель міжгалузевого балансу є основою багатьох лінійних моделей виробничого сектора економіки. Вона базується на понятті «галузь», хоча це поняття не є точно означеним і лише до деякої міри наближає реальну економічну ситуацію. При аналізі за методом «витрати-випуск» основою є балансова таблиця або матриця міжгалузевих потоків, яка охоплює все господарство. На практиці така таблиця складається на основі статистичних звітів. Припустимо, що весь виробничий сектор народного господарства розчленовано на n чистих галузей. Це є умовні галузі, кожна з яких об’єднує все виробництво виду продукції. Чиста галузь є економічною абстракцією, зовсім не обов’язковим є її організаційне оформлення в виді міністерства, об’єднання, тощо. Будемо припускати, що кожна з галузей випускає лише певний продукт, причому різні галузі випускають різні продукти. В процесі виробництва кожна з галузей потребує, взагалі кажучи, продукцію, вироблену в інших галузях. Нехай економіко- виробнича система складається з n галузей, або, інакше кажучи, виробляє n продуктів. Нехай у масштабі народного господарства маємо балансовий звіт за підсумками певного періоду часу за такою формою:
Оскільки таблиця має балансовий характер, то очевидно, можна записати такі співвідношення між параметрами таблиці:
Величини, які тут фігурують, можуть виражатись як в натуральних одиницях виміру (штуки, тони, літри), так і у вартісних. Залежно від цього розділяють натуральний або вартісний міжгалузевий баланс. Якщо всі елементи j -того стовпчика таблиці поділити на величину
Числа aij, j=1,…,n мають назву коефіцієнти прямих витрат j -ї галузі. Вони досить повно характеризують технологію виробництва j -ї галузі за даний період, бо задають об’єм і структуру затрат, необхідних для випуску одиниці j -того продукту. Матриця А=(аij) прямих витрат або технологічна матриця містить в собі інформацію про структуру міжгалузевих зв’язків, про існуючу в даній економіко-виробничій системі технологію виробництва. Якщо розглянути ряд таких матриць, що відповідають різним періодам часу, то будемо мати можливість проаналізувати хід розвитку технології. Матриця А також є дуже корисною в питаннях планування та прогнозування виробництва. Зробимо два важливі припущення: · матриця А є сталою, тобто технологія залишається незмінною на протязі заданого періоду [Т0 , Т], де Т > Т0 . Це може бути, наприклад, рік. · Постулюємо властивість лінійності технологій, тобто вважаємо, що для валового продукції j -ї галузі об’єму хj необхідно і достатньо зробити витрати в об’ємах хj. aij, i=1, …,n продукції всіх галузей. Зроблені припущення є в значній мірі ідеалізацією реального положення справ в економіці. У відповідності до другого припущення маємо: кожна галузь може виробляти будь-який об’єм своєї продукції аби лише була в належній кількості сировина, але ж виробничі потужності кожної галузі обмежені (трудовими ресурсами, основними фондами і т. п.). Матриця А=(аij) описує технологію при роботі всіх галузей з одиничною інтенсивністю. Якщо ж в даний період кожна з n галузей випускає відповідно обсяги x1, x2, …, xn (xj – інтенсивність роботи j-ї газузі) валового випуску відповідно, то вектор інтенсивності x =(x1,x2,…, xn) наз вектором валового випуску. Частка валового випуску, витрачена на виробничі потреби економіки описується вектором виробничих витрат Ax, який дорівнює ( Між векторами виробничих витрат Ax, валового випуску x та вектором споживання c має місце співвідношення x-Ax=c або (I-A)x=c. Отже ми отримали систему x-Ax=c, x>=0 (1) або (I-A)x=c, x>=0, де вектор c>=0, матриця A>=0 відомі. Питання про сумісність системи зводиться до існування невід’ємної оберненої матриці (I-A)-1. Тоді x=(I-A)-1 c>=0. Умова невід’ємності x>=0 ускладнює дослідження системи (1). Система (1), де x, A і c мають вищевказану економічну інтерпретацію називається моделлю Леонтьєва. Означення: Якщо для будь-якого невід’ємного вектора кінцевого попиту c>=0 система (1) сумісна, тобто має розв’язок, то відповідну модель Леонтьєва (або технологічну матрицю A) називають продуктивною. Додамо до моделі (1) двоїсту систему, яка задається в термінах цін. Нехай pi, i=1..n – ціна одиниці продукції і -ї галузі, а p=(p1…pn) – вектор цін. j, j=1,…,n – заробітна плата за одиницю продукції в j-й галузі. w=(w1…wn) – вектор заробітної плати або вектор невиробничих витрат. Тоді твердження: виручка галузі – вартість випуску за цінами реалізації дорівнює її витратам записується у виді p-pA=w p>=0 (2) або p(I-A)=w p>=0 p – вектор рядок. Система (2) є двоїстою до системи (1).
|

 11
11
 1
1
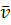 1
1
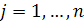 показують розподіл продукції і -ої галузі на виробничі потреби всіх інших галузей.
показують розподіл продукції і -ої галузі на виробничі потреби всіх інших галузей.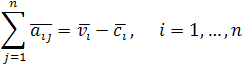
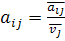 можна розуміти як об’єм продукції і -ї галузі необхідний для виробництва одиниці продукції з номером j; число
можна розуміти як об’єм продукції і -ї галузі необхідний для виробництва одиниці продукції з номером j; число 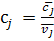 - як долю продукції j -ї галузі витрачену на невиробниче споживання.
- як долю продукції j -ї галузі витрачену на невиробниче споживання. – вектор споживання.
– вектор споживання. ).
).


