Або лінійна модель обміну.
Нехай маємо n країн, які ведуть між собою торгівлю. Позначимо національний прибуток j -ї країни через dj і будемо вважати, що цей прибуток формується з продажу своїх товарів як на внутрішньому, так і на зовнішньому ринку. Структуру торговельних відносин між країнами вважаємо усталеною і частка qi j прибутку dj j -ї країни яка витрачається на імпортування товарів з i -ї країни вважається сталою, зокрема qij не залежить від величини прибутку dj. Розглянемо матрицю Q=(qij), яка описує структуру торгівлі, та вектор прибутків d=(d1…dn). Якщо країни починають торгувати у відповідності до матриці обміну Q, то, очевидно, після одного обороту торгівлі країни матимуть прибуток, який описує вектор Qd: Qd=( Оскільки кожна з країн не бажає зменшити свій прибуток в результаті торгівлі, тому d<=Qd (3). Дослідимо детальніше (3). Оскільки елементи матриці обміну Q=(qij) є частинами прибутку j -ї країни, то, очевидно
Твердження 1. Якщо вектор d задовольняє нерівність (3), то d=Qd. ▼ Доведення. Запишемо (3) в скалярному вигляді
Будемо доводити від супротивного. Нехай при деякому
Маємо протиріччя, що і доводить твердження 1. ▲; Економічне тлумачення твердження 1: Якщо при функціонуванні розглянутої моделі обміну хтось збагатився, то це обов’язково за рахунок когось із партнерів. Тому природно виникає питання про існування і обчислення такого вектора прибутків країн-партнерів d, який справджує рівняння d=Qd в твердженні 1. Необхідна умова полягає в існуванні серед власних чисел матриці Q числа 1. Далі виникає питання про існування відповідного невід’ємного власного вектора. Ще одне цікаве і важливе питання виникає при аналізі моделі обміну: якщо система функціонує з матрицею Q k турів, то маємо на кожному кроці (турі) такі вектори прибутків d, Qd, Q2d, Q3d, …, Qkd. Цікаво дослідити асимптотику, при k Для відповіді на ці та інші питання використовуємо апарат спеціального розділу теорії матриць – теорії невід’ємних матриць.
|

 ).
). j=1..n (4)
j=1..n (4)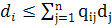 i=1..n (5)
i=1..n (5) нерівність (5) є строгою. Враховуючи це, отримаємо суму
нерівність (5) є строгою. Враховуючи це, отримаємо суму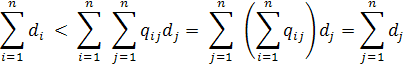
 (
( ) поведінку вектора прибутків.
) поведінку вектора прибутків.


