Теорема Фробеніуса-Перрона Нерозкладна матриця A має додатнє власне значення  a таке, що модулі всіх решта власних чисел не перевищують
a таке, що модулі всіх решта власних чисел не перевищують  a:
a:
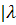 k| ≤;
k| ≤;  , k = 1,…,m.
, k = 1,…,m.
Числу  a відповідає єдиний (з точністю до скалярного множника) власний вектор XA, всі координати якого ненульові і одинакові за знаком:
a відповідає єдиний (з точністю до скалярного множника) власний вектор XA, всі координати якого ненульові і одинакові за знаком:
Sign(XA)I = Sign(XA)j ,  i,j = 1
i,j = 1  n.
n.
Тобто вектор XA можна вибрати додатнім XA > 0.
Зазначимо, що число  a називається числом Фробеніуса, а вектор XA – вектором Фробеніуса матриці A (Axa =
a називається числом Фробеніуса, а вектор XA – вектором Фробеніуса матриці A (Axa =  a xa;
a xa;  a – розв’язок рівняння det(A-
a – розв’язок рівняння det(A- 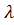 I) = 0).
I) = 0).
Теорема 2. Якщо квадратна n*n матриця A невід’ємна, то вона має невід’ємне власне число  a ≥ 0 таке, що для будь-якого іншого її власного числа
a ≥ 0 таке, що для будь-якого іншого її власного числа  має місце нерівність |
має місце нерівність | 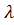 | ≤
| ≤  a. При цьому існує невід’ємний власний вектор XA ≥ 0, який відповідає
a. При цьому існує невід’ємний власний вектор XA ≥ 0, який відповідає  .
.
Для формулювання наступної теореми введемо позначення:



 a таке, що модулі всіх решта власних чисел не перевищують
a таке, що модулі всіх решта власних чисел не перевищують 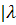 k| ≤;
k| ≤;  , k = 1,…,m.
, k = 1,…,m. i,j = 1
i,j = 1  n.
n. a – розв’язок рівняння det(A-
a – розв’язок рівняння det(A- 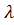 I) = 0).
I) = 0). .
.




