Означення. Нерозкладна матриця А, яка не є циклічною, називається примітивною.
Зауважимо, що одночасною перестановкою рядків і стовпців циклічної матриці А її можна звести до вигляду
, де розміри квадратного блока Теорема. Якщо матриця примітивна, то вона стійка. Теорема. (Ознака стійкості невід’ємної матриці в залежності від її власних чисел). Для того, щоб нерозкладна матриця
Аналіз продуктивності моделі «затрати-випуск» Виявляється, що продуктивність моделі Леонтьєва повністю визначається величиною числа Фробеніуса Теорема 1. (Критерій продуктивності моделі «витрати-випуск»). Для продуктивності моделі Леонтьєва
необхідно і достатньо, щоб Фробеніусове власне число ▼Достатність. Покажемо, що при *) **) існує Маємо Запишемо тотожність, справедливу для довільної квадратної матриці А:
Перейдемо в (2) до границі при
Ми отримали матричний варіант формули для суми нескінченно спадної Оскільки при будь-якому
Отже, модель Леонтьєва є продуктивною. Необхідність. Припускаючи, що модель Леонтьєва продуктивна, робимо висновок про існування такого вектора Нехай при цьому вектор
тобто Оскільки ▲; Отже, перевірка моделі Леонтьєва на продуктивність звелась до чисто математичної задачі оцінки власних чисел матриці А. Тепер сформулюємо деякі достатні ознаки продуктивності безпосередньо в термінах параметра моделі (1). Теорема 2. (Достатня умова продуктивності моделі «затрати-випуск»). Нехай система (1) має розв’язок при деякому Тоді модель Леонтьєва продуктивна. Іншими словами, якщо деякий додатній кінцевий попит можна задовольнити в моделі Леонтьєва (1), то вона продуктивна. ▼; Міркуючи так, які при доведенні необхідності в теоремі 1, будемо мати ▲; Теорема 3. (Достатні умови продуктивності моделі «витрати-випуск»). Нехай 1) матриця 2) сума
3) хоча б для одного рядка Тоді модель Леонтьєва, яка відповідає цій матриці, є продуктивною. ▼; Доведення. Нехай
Але, крім цього
Отже, знову ▲; Економічне тлумачення теореми 3. Нехай ми розглядаємо міжгалузевий баланс в натурально-вартісній формі. Отже, елемент
x – Ax = с x >= 0 x = (I – A)-1с = ( Прокоментуємо цю формулу, з якої, за умови продуктивності моделі, можна знайти за відомим кінцевим попитом с валовий продукт х. Щоб дістати вектор с >= 0 кінцевого попиту необхідно виробити всю кількість продукції, яку описується компонентами цього вектора (I додаток – с) але в процесі виробництва с виникають витрати Aс – II додаток, в свою чергу, для виробництва Ас знову маємо виробничі витрати А2с = ААс і т.д. тому ряд (I – А)-1с = с + Ас + А2с + … називається повними витратами на виробництво продукту, а матрицю (I – А)-1 називаємо матрицею повних витрат. Повернемось до моделі міжнародної торгівлі. Вияснимо поведінку векторів прибутку d з моделі, яка описується рівнянням Qd = d. Оскільки для матриці Q повинна виконуватись умова, що сума елементів кожного стовпця рівна 1, то з теореми про область зміни фробеніусового числа маємо Отже, якою торгівля починається в умовах, коли початковий розподіл прибутків співпадає з одним з векторів Фробеніуса dQ, то внаслідок такої торгівлі прибутки країн не змінюватимуться: d = dQ (Q dQ = dQ) і послідовність dQ, dQ … dQ є стаціонарною. Якщо починаємо торгівлю з довільного початкового вектора d0, то зміна вектора прибутків d(k) = Qkd0 залежить від властивостей матриці Q. Якщо Q нерозкладна і примітивна, то вона стійка, тобто
|


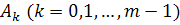 співпадають із кількістю елементів у множині
співпадають із кількістю елементів у множині 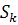 .
. була стійкою, необхідно і достатньо, щоб всі її власні числа
була стійкою, необхідно і достатньо, щоб всі її власні числа 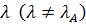 знаходилися всередині круга радіуса
знаходилися всередині круга радіуса  :
: 
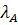 матриці А коефіцієнтів прямих затрат.
матриці А коефіцієнтів прямих затрат. (1)
(1)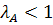 .
. модель (1) продуктивна. Для цього покажемо, що
модель (1) продуктивна. Для цього покажемо, що ,
, .
.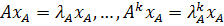 , отже
, отже  , бо
, бо  , то твердження (*) доведено.
, то твердження (*) доведено.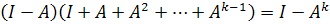 (2)
(2) . Границя правої частини існує і дорівнює І. Тому
. Границя правої частини існує і дорівнює І. Тому  . Отже ряд
. Отже ряд 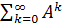 збігається і його сума представляє собою матрицю
збігається і його сума представляє собою матрицю  :
: (3)
(3) геометричної прогресії.
геометричної прогресії.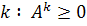 , то матриця
, то матриця  система (1) має розв’язок
система (1) має розв’язок (4)
(4)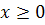 , що
, що  .
.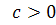 , тоді
, тоді 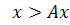 . Помножимо останню нерівність скалярно на вектор
. Помножимо останню нерівність скалярно на вектор 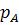 :
:
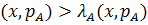 .
. , то звідси
, то звідси 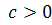 .
.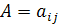 невід’ємна і нерозкладна;
невід’ємна і нерозкладна; елементів кожногоi-го рядка не перевищує 1:
елементів кожногоi-го рядка не перевищує 1: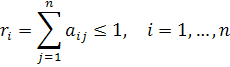
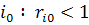 .
. . Тоді будемо мати
. Тоді будемо мати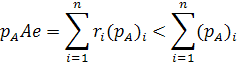

 , тобто
, тобто 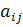 матриці А означає на яку суму j-та галузь витрачає продукцію i-ї галузі в розрахунку на 1 грн своєї продукції. Тоді
матриці А означає на яку суму j-та галузь витрачає продукцію i-ї галузі в розрахунку на 1 грн своєї продукції. Тоді  виражає сумарну величину витрат продукції і-ї галузі всіма галузями при умові, що кожна з них випускає продукції на 1 грн. Умова
виражає сумарну величину витрат продукції і-ї галузі всіма галузями при умові, що кожна з них випускає продукції на 1 грн. Умова  означає, що і -та галузь здатна задовольнити потреби всіх галузей. Однак тільки цієї умови замало, бо матриця
означає, що і -та галузь здатна задовольнити потреби всіх галузей. Однак тільки цієї умови замало, бо матриця 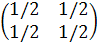 не є продуктивною.
не є продуктивною. ) с = с + Aс + A2с + …
) с = с + Aс + A2с + … Q = 1.
Q = 1. , тобто ми отримали dk =
, тобто ми отримали dk = 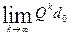 =
= 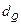 .
.


