Модель динамічного міжгалузевого балансу.
Модель Леонтьєва, яку ми розглядали дотепер - статична, тобто в ній не враховано фактор часу. Для того, щоб ефективно вивчати розгорнуті в часі виробничі процеси, слід узагальнити модель Леонтьєва, при цьому доцільно підходити диференційовано до різних галузей господарства, бо є галузі (це в першу чергу галузі фондоутворення – будівництво і машинобудування), які порівняно з іншими мають більший вплив на динаміку розвитку економіки. При побудові багатогалузевих динамічних моделей необхідно врахувати ще і явище запізнення (так званий часовий лаг). Сформульованим вимогам задовольняють в значній мірі модель динамічного багатогалузевого балансу (або π-модель), а також модель Неймана, яку розглянемо далі. Динамічна модель Леонтьєва є частковим випадком моделі Неймана. Розглянемо економіку, яка виробляє і споживає n типів товарів. Нехай сукупний запас товарів описується n -вимірним вектором x = (x1, …, xn). Технологічні витрати кожної галузі при роботі з одиничною інтенсивністю задамо леонтієвською матрицею А. Введемо ряд необхідних понять і означень. Через
Dη;, де dij – витрати i-го товару на одиничний приріст j-ї галузі При цьому числа d1jhj, d2jhj, …, dnjhj показують витрати кожного з товарів необхідні для збільшення потужності j -ої галузі. Введемо число lj трудових затрат, необхідних для випуску одиниці продукції галузі з номером j, а також вектор (l = l1, l2, …, ln), який будемо називати вектором трудових затрат. Літерою L позначимо загальну кількість найнятих робітників. Нехай с = (с1, …,сn) вектор споживання розрахований на одного працівника, його “натуральна” заробітна плата. Тоді один з можливих варіантів схеми динамічного міжгалузевого балансу (так звана π-модель) можна подати в такому вигляді: 1. Необхідність дотримання матеріального балансу: якщо в період [ t-1, t ] план описується вектором (xt, ξt, ηt, Lt) ∊ Axt + Dηt + Ltс ≤ xt (1) 2. В кожному з періодів t = 1,2,…,Т валовий випуск обмежений (обмеження зумовлене наявними на цей момент основними потужностями): xt ≤ ξt-1 (2) 3. Динаміка приросту основних потужностей очевидна: ξt - ξt-1 ≤ ηt (3) 4. Обмеження на об’єм трудових ресурсів, які зайняті в процесі виробництва: (l, xt) ≤ Lt (4) 5. Невід’ємність кожної зі змінних: (xt, ξt, ηt, Lt) ≥ 0 (5) При цьому в кожному із співвідношень t = 1,2,…,Т, а ξ0 – основні потужності галузей, створені на початок процесу. Модель (1) – (5) є безумовно змістовнішою ніж статична модель Леонтьєва. Ця модель є динамічною і в результаті її функціонування ми одержимо деяку послідовність векторів (xt, ξt, ηt, Lt), t = 1,2,…,Т, яка задовільняє всі обмеження моделі. Таку послідовність будемо називати траекторією. В кінці досліджуваного періоду (в момент часу Т) стан моделі характеризується вектором (xТ, ξТ, ηТ, LТ) (так званий термінальний стан моделі). Нехай С1, С2, С3 – задані n -мірні вектори, а С4 – скаляр. Введемо до розгляду функціонал: І = (С1, xТ) + (С2, ξТ) + (С3, ηТ) + С4 LТ (6) і поставимо для моделі (1) – (5) таку оптимізаційну задачу: серед всіх траекторій моделі (1) – (5) знайти таку, яка максимізує функціонал (6). При цьому вектор основних потужностей в початковому стані ξ0 і коефіцієнти термінального функціоналу (С1, С2, С3, С4) задані. Описану модель можна подати в компактному записі. Якщо покласти:
то модель (1) – (6) набуває вигляду: (с, хТ) → max
|

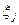 – позначимо максимально можливий валовий випуск галузі з номером j. Тоді вектор
– позначимо максимально можливий валовий випуск галузі з номером j. Тоді вектор 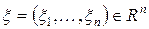 описує сукупний максимально можливий валовий випуск.
описує сукупний максимально можливий валовий випуск.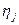 – бажаний приріст основної потужності j -ї галузі. Якщо розглянути n -мірний вектор
– бажаний приріст основної потужності j -ї галузі. Якщо розглянути n -мірний вектор 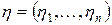 , то матеріальні затрати на приріст основних потужностей всіх галузей будуть дорівнювати вектору
, то матеріальні затрати на приріст основних потужностей всіх галузей будуть дорівнювати вектору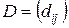 ,
, 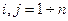 .
.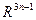 , то в сумі об’єм біжучих виробничих затрат (Axt), затрат на фондоутворення (Dξt) і заробітної плати Ltс не може перевищувати валового випуску в даному періоді:
, то в сумі об’єм біжучих виробничих затрат (Axt), затрат на фондоутворення (Dξt) і заробітної плати Ltс не може перевищувати валового випуску в даному періоді: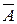 =
= 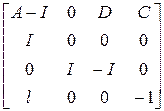 ,
, 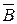 =
=  ,
,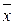 = (x, ξ;, η;, L),
= (x, ξ;, η;, L), 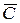 = (С1, С2, С3, С4) ∊
= (С1, С2, С3, С4) ∊ 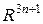
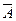
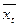 ≤
≤ 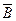
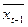
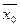 = (0, ξ0, 0, 0) – заданий вектор
= (0, ξ0, 0, 0) – заданий вектор


