Означення 1. Будемо говорити що модель Неймана знаходиться в стані динамічної рівноваги 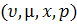 , де числа
, де числа  , n- вимірні вектори
, n- вимірні вектори  , якщо виконані умови:
, якщо виконані умови:
γ  ,
,
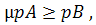
 (1)
(1)
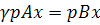
Число  є не що інше як вартість затрат в стані рівноваги моделі Неймана, складовими якого є вектори інтенсивностей
є не що інше як вартість затрат в стані рівноваги моделі Неймана, складовими якого є вектори інтенсивностей  та цін
та цін 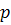 . Природно вважати що
. Природно вважати що 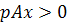 тоді з двох останніх рівностей (1) будемо мати
тоді з двох останніх рівностей (1) будемо мати  α.
α.
Означення 2. Трійка 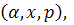 де число
де число 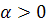 ,
,
вектори 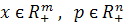 такі, що
такі, що
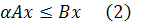
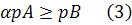
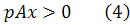
називають невиродженим положенням рівноваги моделі Неймана.
Означення 3. Число α, яке фігурує в невиродженому положенні рівноваги (2) – (4) моделі Неймана  називається темпом росту
називається темпом росту
Означення 4 Розглянемо множину векторів (промінь) 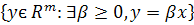 , де
, де  є компонентою невиродженого положення рівноваги. Такий промінь називають променем Неймана.
є компонентою невиродженого положення рівноваги. Такий промінь називають променем Неймана.
Цікаво знати, чи має система (2)(3)(4) розв’язок, тобто, чи існує невироджене положення рівноваги моделі Неймана, породженої парою матриць  При певних обмеженнях на ці матриці, відповідь на це питання містить теорема 1.
При певних обмеженнях на ці матриці, відповідь на це питання містить теорема 1.
Теорема 1. (Умова існування не виродженого положення рівноваги моделі Неймана). Нехай невід’ємні матриці  такі, що матриця випуску
такі, що матриця випуску 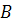 не містить нульових рядків, а матриця затрат
не містить нульових рядків, а матриця затрат 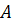 не містить нульових стовпчиків. Тоді відповідна модель Неймана має невироджене положення рівноваги. Інакше кажучи, система (2-4) має розв’язок.
не містить нульових стовпчиків. Тоді відповідна модель Неймана має невироджене положення рівноваги. Інакше кажучи, система (2-4) має розв’язок.
Умови теореми допускають прозоре економічне тлумачення:
*) Умова  означає,що ми не маємо серед базисних процесів таких, які нічого не витрачають (відсутній «ріг достатку»).
означає,що ми не маємо серед базисних процесів таких, які нічого не витрачають (відсутній «ріг достатку»).
*) Умова  означає, що в нашій системі (система замкнута!) виробляється всякий продукт.
означає, що в нашій системі (система замкнута!) виробляється всякий продукт.
▼Доведення
Спочатку розглянемо допоміжну задачу лінійного програмування
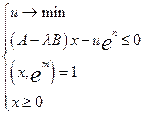 (5)
(5)
де  - числовий параметр,
- числовий параметр,
 - змінні задачі,
- змінні задачі,
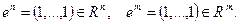
Лема 1:Якщо 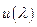 - значення задачі (5), то:
- значення задачі (5), то:
(*). 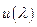 - неперервна функція, залежна від параметра
- неперервна функція, залежна від параметра  ;
;
(**)  ;
;
(***)  , якщо
, якщо 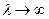 ;
;
(****) 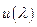 - монотонна незростаюча функція;
- монотонна незростаюча функція;
▼Доведення
Нехай  . Множина Х, очевидно, обмежена і замкнена. Значить і множина
. Множина Х, очевидно, обмежена і замкнена. Значить і множина  також обмежена і замкнена множина.
також обмежена і замкнена множина.
Значення задачі (5) має вигляд:
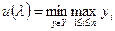 (6)
(6)
Існування такого скінченного  випливає з обмеженості і замкнутості множини
випливає з обмеженості і замкнутості множини  . Тобто для будь-якого
. Тобто для будь-якого  задача лінійного програмування (5) має розв’язок
задача лінійного програмування (5) має розв’язок 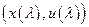 , тобто функція
, тобто функція 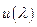 визначена на всій дійсній осі.
визначена на всій дійсній осі.
Неперервність цієї функції випливає з загальних властивостей задач лінійного програмування, залежних від параметра.
Властивість (**) рівносильна твердженню  :
: 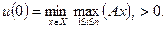
Дійсно, якщо  такий, що
такий, що  , то це неможливо, бо за умовою матриця витрат А не має нульових стовпчиків.
, то це неможливо, бо за умовою матриця витрат А не має нульових стовпчиків.
Властивість (***) легко вивести безпосередньо. Виберемо  , тоді
, тоді 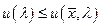 .
.
З другого боку
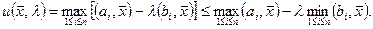
Нагадаємо, що в матриці В немає нульових стрічок, тобто  . Звідси і випливає необхідне твердження, що
. Звідси і випливає необхідне твердження, що 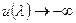 при
при 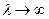 .
.
Четверта властивість (****) є наслідком умови  :
:
 для будь-яких
для будь-яких  .
.
Лема доведена. ▲
Зазначимо, що функція  може бути обмежена зверху.
може бути обмежена зверху.
З встановлених властивостей функції 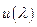 випливає існування такого
випливає існування такого  , для якого
, для якого 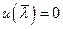 . Якщо
. Якщо 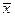 відповідний розв’язок задачі (5), то
відповідний розв’язок задачі (5), то
 ,
,  (7)
(7)
Розглянемо задачу, двоїсту до (5):
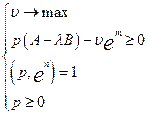 (8)
(8)
З теореми двоїстості маємо 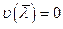 . Якщо при цьому
. Якщо при цьому 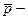 відповідний розв’язок задачі (8), то
відповідний розв’язок задачі (8), то 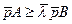 ,
, 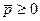 (9)
(9)
З нерівностей (7) і (9) бачимо, що знайдена трійка 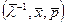 є положенням рівноваги моделі Неймана, хоча, можливо, це не є невироджений випадок.
є положенням рівноваги моделі Неймана, хоча, можливо, це не є невироджений випадок.
Значення 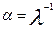 будемо називати темпом росту.
будемо називати темпом росту.

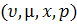 , де числа
, де числа  , n- вимірні вектори
, n- вимірні вектори  , якщо виконані умови:
, якщо виконані умови: ,
,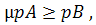
 (1)
(1)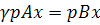
 є не що інше як вартість затрат в стані рівноваги моделі Неймана, складовими якого є вектори інтенсивностей
є не що інше як вартість затрат в стані рівноваги моделі Неймана, складовими якого є вектори інтенсивностей  та цін
та цін 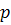 . Природно вважати що
. Природно вважати що 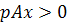 тоді з двох останніх рівностей (1) будемо мати
тоді з двох останніх рівностей (1) будемо мати  α.
α.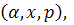 де число
де число 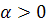 ,
,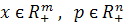 такі, що
такі, що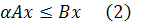
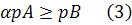
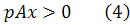
 називається темпом росту
називається темпом росту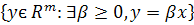 , де
, де  є компонентою невиродженого положення рівноваги. Такий промінь називають променем Неймана.
є компонентою невиродженого положення рівноваги. Такий промінь називають променем Неймана. При певних обмеженнях на ці матриці, відповідь на це питання містить теорема 1.
При певних обмеженнях на ці матриці, відповідь на це питання містить теорема 1. такі, що матриця випуску
такі, що матриця випуску 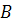 не містить нульових рядків, а матриця затрат
не містить нульових рядків, а матриця затрат 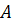 не містить нульових стовпчиків. Тоді відповідна модель Неймана має невироджене положення рівноваги. Інакше кажучи, система (2-4) має розв’язок.
не містить нульових стовпчиків. Тоді відповідна модель Неймана має невироджене положення рівноваги. Інакше кажучи, система (2-4) має розв’язок. означає,що ми не маємо серед базисних процесів таких, які нічого не витрачають (відсутній «ріг достатку»).
означає,що ми не маємо серед базисних процесів таких, які нічого не витрачають (відсутній «ріг достатку»). означає, що в нашій системі (система замкнута!) виробляється всякий продукт.
означає, що в нашій системі (система замкнута!) виробляється всякий продукт.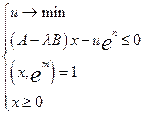 (5)
(5) - числовий параметр,
- числовий параметр, - змінні задачі,
- змінні задачі,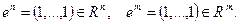
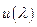 - значення задачі (5), то:
- значення задачі (5), то: ;
; ;
; , якщо
, якщо 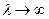 ;
; . Множина Х, очевидно, обмежена і замкнена. Значить і множина
. Множина Х, очевидно, обмежена і замкнена. Значить і множина  також обмежена і замкнена множина.
також обмежена і замкнена множина.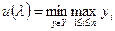 (6)
(6) випливає з обмеженості і замкнутості множини
випливає з обмеженості і замкнутості множини  . Тобто для будь-якого
. Тобто для будь-якого  задача лінійного програмування (5) має розв’язок
задача лінійного програмування (5) має розв’язок 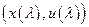 , тобто функція
, тобто функція  :
: 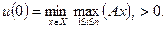
 такий, що
такий, що  , то це неможливо, бо за умовою матриця витрат А не має нульових стовпчиків.
, то це неможливо, бо за умовою матриця витрат А не має нульових стовпчиків. , тоді
, тоді 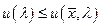 .
.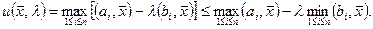
 . Звідси і випливає необхідне твердження, що
. Звідси і випливає необхідне твердження, що 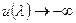 при
при  :
: для будь-яких
для будь-яких  .
. може бути обмежена зверху.
може бути обмежена зверху. , для якого
, для якого 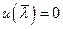 . Якщо
. Якщо 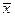 відповідний розв’язок задачі (5), то
відповідний розв’язок задачі (5), то ,
,  (7)
(7)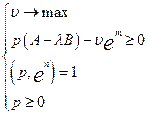 (8)
(8)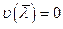 . Якщо при цьому
. Якщо при цьому 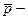 відповідний розв’язок задачі (8), то
відповідний розв’язок задачі (8), то 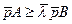 ,
, 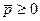 (9)
(9)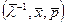 є положенням рівноваги моделі Неймана, хоча, можливо, це не є невироджений випадок.
є положенням рівноваги моделі Неймана, хоча, можливо, це не є невироджений випадок.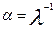 будемо називати темпом росту.
будемо називати темпом росту.


