Це означає, що для виробництва в період [ t, t+1 ] ми можемо витрачати лише продукцію вироблену в попередньому періоді [ t-1, t ]. Позаяк випуск в період [ t-1, t ] є Вх  , а витрати в наступний період є Ах
, а витрати в наступний період є Ах  , то припущення про замкнутість набуває такого вигляду
, то припущення про замкнутість набуває такого вигляду
Ах  ≤ Вх
≤ Вх  , t = 1,2,…,Т (3)
, t = 1,2,…,Т (3)
Це є послідовність векторних нерівностей. При цьому природно вважати, що вектор Вх  є вектором запасів, які є в нашому розпорядженні з початку досліджуваного періоду [ 1, Т ].
є вектором запасів, які є в нашому розпорядженні з початку досліджуваного періоду [ 1, Т ].
Означення1. Послідовність векторів інтенсивностей  , які задовольняють систему нерівностей (3) будемо називати планом або траекторією інтенсивностей.
, які задовольняють систему нерівностей (3) будемо називати планом або траекторією інтенсивностей.
Введемо в модель ще поняття цін на товари. Через  позначимо ціну одиниці
позначимо ціну одиниці  -го продукту в період [t-1,t], а відповідний n-вимірний вектор цін через
-го продукту в період [t-1,t], а відповідний n-вимірний вектор цін через 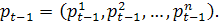
Прибуток процесу (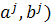 за період [t-1,t] виражається як (
за період [t-1,t] виражається як (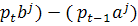 . При цьому ми вважаємо на початку періоду [t-1,t] ціну на сировину
. При цьому ми вважаємо на початку періоду [t-1,t] ціну на сировину  рівною
рівною 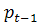 , а випущену продукцію
, а випущену продукцію  реалізуємо вже за цінами нового періоду
реалізуємо вже за цінами нового періоду 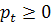
Припущення 3. Жоден з базисних процесів 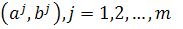 не дає додатного прибутку
не дає додатного прибутку

тобто

Це припущення називається практикою нульового прибутку або практикою безпродуктовості виробництва. Це припущення дещо парадоксальне. Воно містить своєрідну вимогу щодо замкнутості моделі: із зростанням загального числа товарів грошова маса не збільшується.
Означення 2. Послідовність {  векторів цін, які задовольняють систему нерівностей (4) будемо називати траєкторією цін.
векторів цін, які задовольняють систему нерівностей (4) будемо називати траєкторією цін.
Припущення 4. Загальна грошова маса не змінюється і весь час знаходиться в обігу тобто
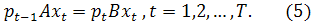
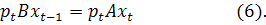
Означення 3. Траекторія інтенсивностей { 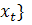 називається стаціонарною, якщо для деякого υ>0,
називається стаціонарною, якщо для деякого υ>0,  υ
υ  , тобто
, тобто  є геометричною прогресією із знаменником υ:
є геометричною прогресією із знаменником υ:  .
.
Означення 4. Траекторія цін { 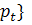 називається стаціонарною, якщо для деякого µ> 0 маємо
називається стаціонарною, якщо для деякого µ> 0 маємо  , тобто
, тобто 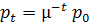 .
.
Підставимо вирази  та
та  в векторні нерівності (3) та (4) відповідно. Приходимо до таких тверджень:
в векторні нерівності (3) та (4) відповідно. Приходимо до таких тверджень:
(a) Послідовність інтенсивностей 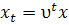 буде стаціонарною тоді і тільки тоді, коли для числа υ>0 і початкового вектора
буде стаціонарною тоді і тільки тоді, коли для числа υ>0 і початкового вектора  справедлива нерівність
справедлива нерівність
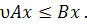 (7)
(7)
(b) Послідовність цін 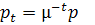 буде стаціонарною траєкторією цін тоді і тільки тоді, коли
буде стаціонарною траєкторією цін тоді і тільки тоді, коли 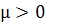 і початковий вектор
і початковий вектор  справджують нерівність µ
справджують нерівність µ  . (8)
. (8)
Зазначимо нарешті, що для стаціонарних траєкторій 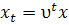 ,
, 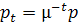 співвідношення (5), (6) з припущенням (3) набувають такого вигляду:
співвідношення (5), (6) з припущенням (3) набувають такого вигляду:
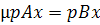 (9)
(9)
 (10).
(10).
Таким чином, динамічна модель фон Неймана математично описується нерівностями (7), (8) і рівностями (9), (10).

 , а витрати в наступний період є Ах
, а витрати в наступний період є Ах  , то припущення про замкнутість набуває такого вигляду
, то припущення про замкнутість набуває такого вигляду є вектором запасів, які є в нашому розпорядженні з початку досліджуваного періоду [ 1, Т ].
є вектором запасів, які є в нашому розпорядженні з початку досліджуваного періоду [ 1, Т ]. , які задовольняють систему нерівностей (3) будемо називати планом або траекторією інтенсивностей.
, які задовольняють систему нерівностей (3) будемо називати планом або траекторією інтенсивностей. позначимо ціну одиниці
позначимо ціну одиниці  -го продукту в період [t-1,t], а відповідний n-вимірний вектор цін через
-го продукту в період [t-1,t], а відповідний n-вимірний вектор цін через 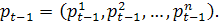
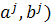 за період [t-1,t] виражається як (
за період [t-1,t] виражається як (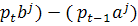 . При цьому ми вважаємо на початку періоду [t-1,t] ціну на сировину
. При цьому ми вважаємо на початку періоду [t-1,t] ціну на сировину  рівною
рівною 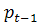 , а випущену продукцію
, а випущену продукцію  реалізуємо вже за цінами нового періоду
реалізуємо вже за цінами нового періоду 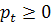
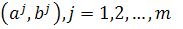 не дає додатного прибутку
не дає додатного прибутку

 векторів цін, які задовольняють систему нерівностей (4) будемо називати траєкторією цін.
векторів цін, які задовольняють систему нерівностей (4) будемо називати траєкторією цін.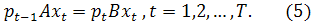
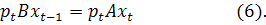
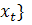 називається стаціонарною, якщо для деякого υ>0,
називається стаціонарною, якщо для деякого υ>0,  υ
υ  , тобто
, тобто  є геометричною прогресією із знаменником υ:
є геометричною прогресією із знаменником υ:  .
.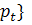 називається стаціонарною, якщо для деякого µ> 0 маємо
називається стаціонарною, якщо для деякого µ> 0 маємо  , тобто
, тобто 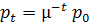 .
. та
та  в векторні нерівності (3) та (4) відповідно. Приходимо до таких тверджень:
в векторні нерівності (3) та (4) відповідно. Приходимо до таких тверджень: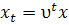 буде стаціонарною тоді і тільки тоді, коли для числа υ>0 і початкового вектора
буде стаціонарною тоді і тільки тоді, коли для числа υ>0 і початкового вектора  справедлива нерівність
справедлива нерівність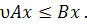 (7)
(7)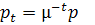 буде стаціонарною траєкторією цін тоді і тільки тоді, коли
буде стаціонарною траєкторією цін тоді і тільки тоді, коли 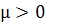 і початковий вектор
і початковий вектор  справджують нерівність µ
справджують нерівність µ  . (8)
. (8)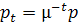 співвідношення (5), (6) з припущенням (3) набувають такого вигляду:
співвідношення (5), (6) з припущенням (3) набувають такого вигляду: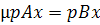 (9)
(9) (10).
(10).


