Порівняльна статика моделі Леонтьєва
Повернемось знову до звичайної моделі Леонтьєва
Координати Матриця А вважається при цьому фіксованою. По суті, мова йде про реакцію системи з технологічною матрицею А на зміну зовнішніх або екзотичних параметрів - координат вектора попиту. Теорема 1 (про додатність вектора валового випуску в нерозкладній продуктивній моделі Леонтьєва). Нехай в моделі (1) матриця А нерозкладна і продуктивна, вектор попиту с Тоді ▼; Доведення: Для
Виберемо номер ▲; Нехай в моделі (1) в вектора попиту с збільшили першу координату Теорема 2 (про реакцію валового випуску в моделі Леонтьєва на зміну вектора попиту). Нехай матриця А ≥ 0 в моделі (1) нерозкладна і продуктивна. Якщо
Причому, якщо максимум в (3) досягається крім j= 1щедля якогось j=i, тобто якщо
▼; Доведення: Позначимо Тоді
Позначимо Для всякого і за означенням
Підставляючи в даний вираз
або Нехай Від супротивного: припустимо, що 1
звідки, врахувавши (4), маємо
що суперечить означенню Таким чином, якщо 1 Отже, 1 Припустимо, що i ▲;
Означення Набір векторів (p*, w*, x*, r*, c*) називається станом рівноваги при заданих А, В і функціях попиту c(p, w) та пропозиції r(p, w) якщо виконуються такі умови: x* = A x* + c* B x* ≤ r* p*A + w*B ≥ p* (6) c* = c(p*, w*) r* = r(p*, w*) Очевидно, що рівноважний валовий випуск x* є розв’язком задачі лінійного програмування (2), а рівноважні ціни на фактори w* - розв’язком двоїстої до неї задачі (3). За теорією двоїстості лінійного програмування значення цих задач рівні, (p*, c*) = (w*, r*), де (p*, c*) – максимальна вартість кінцевої продукції, а (w*, r*) – мінімальна вартість первісних факторів. Таким чином, у стані рівноваги національний продукт = національному доходу. Згідно теорії двоїстості, якщо обмеження задовольняються в точці розв’язку як строга нерівність, то відповідні двоїсті змінні в оптимальному плані є нульовими. Таким чином для прямої задачі (1) маємо
Ця умова означає, що коли загальний попит на фактор менший наявної пропозиції, то оптимальна оплата цього фактора нульова. Тому підхід лінійного програмування до загальної рівноваги поширюється не тільки на дефіцитні фактори, що мають додатню оплату, але також на вільні фактори, оплата яких = нулю Для двоїстої задачі аналогічні умови (доповнювальної нежорсткості) записуються таким чином: для j=1, …, n якщо
Тобто, коли товар вироблений із збитком (тобто середні витрати на виробництво, що дорівнюють лівій частині нерівності у твердженні (8), перевищують ціну), то тоді оптимальний випуск цього товару – нульовий, тобто товар не виробляється. Таким чином, підхід лінійного програмування до загальної рівноваги охоплює не тільки товари, що виробляються (при середніх витратах виробництва рівних ціні), але й товари, що не виробляються. Теорема. Якщо функція попиту c(p, w), функція пропозиції r(p, w) однозначні та неперервні для довільних цін p ≥ 0, w ≥ 0, то стан рівноваги (6) в економіці існує.
|

 (1)
(1)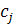 вектора кінцевого попиту можна розглядати як параметри системи (1) і ставити математичну задачу про характер залежності розв’язку х від вектора с: х=х(с).
вектора кінцевого попиту можна розглядати як параметри системи (1) і ставити математичну задачу про характер залежності розв’язку х від вектора с: х=х(с).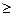 0, c ≠ 0.
0, c ≠ 0. . Інакше, в нерозкладній продуктивній виробничій системі для задоволення ненульового кінцевого попиту необхідний валовий випуск кожного з товарів в додатній кількості.
. Інакше, в нерозкладній продуктивній виробничій системі для задоволення ненульового кінцевого попиту необхідний валовий випуск кожного з товарів в додатній кількості. можемо записати:
можемо записати: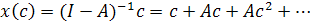 (2)
(2)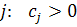 . Тоді за властивостями нерозкладних матриць
. Тоді за властивостями нерозкладних матриць 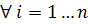 знайдеться натуральне k таке, що
знайдеться натуральне k таке, що 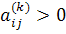 . Тоді
. Тоді 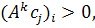 а отже і
а отже і 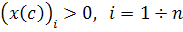 .
. (попит на перший товар зріс), а всі інші координати не змінили, тобто попит на всі інші товари не змінився. Як прореагує на це система і яким буде вектор валового випуску х(с)?
(попит на перший товар зріс), а всі інші координати не змінили, тобто попит на всі інші товари не змінився. Як прореагує на це система і яким буде вектор валового випуску х(с)?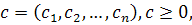 а
а 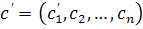 , причому
, причому 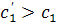 , то
, то (3)
(3)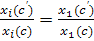 при i ≠ 1, то необхідно
при i ≠ 1, то необхідно 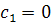 .
.  . Вже відомо, що
. Вже відомо, що  .
.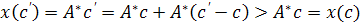 .
.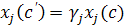 . З нерівності
. З нерівності 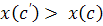 випливає що
випливає що 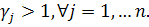
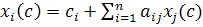 .
.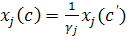 отримаємо
отримаємо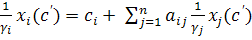 ,
, . (4)
. (4) . Покажемо, що 1
. Покажемо, що 1  S. Тоді (3) буде доведено.
S. Тоді (3) буде доведено. . Тоді
. Тоді  виконується умова
виконується умова  ,
,  при
при 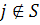 . Тому, якщо серед чисел
. Тому, якщо серед чисел 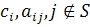 знайдуться ненульові, то оскільки
знайдуться ненульові, то оскільки 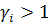 , отримаємо
, отримаємо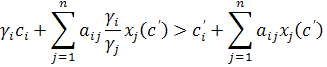
 , (5)
, (5) .
.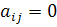 як тільки
як тільки 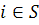 ,
,  . Оскільки
. Оскільки  , то
, то 
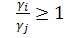 , при j=1,2,…,n. При цих припущеннях знову з (4) випливає (5). Тому
, при j=1,2,…,n. При цих припущеннях знову з (4) випливає (5). Тому  .
. (7)
(7)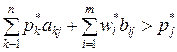 , то
, то 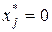 (8)
(8)


