В моделі фон Неймана розглядається скінченний набір виробничих процесів вигляду (a 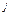 , b
, b 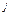 ), j = 1,…,m, де n -вимірний вектор a
), j = 1,…,m, де n -вимірний вектор a 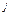 =(а
=(а 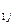 , а
, а  ,…, а
,…, а  ) описує витрати, а n -вимірний вектор b
) описує витрати, а n -вимірний вектор b 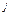 =(b
=(b 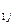 , b
, b  ,…, b
,…, b  ) описує випуск продукції при функціонуванні даного процесу з одиничною інтенсивністю. Виробничі процеси (a
) описує випуск продукції при функціонуванні даного процесу з одиничною інтенсивністю. Виробничі процеси (a 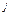 , b
, b 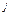 ) будемо називати базисними. Координати векторів a
) будемо називати базисними. Координати векторів a 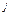 , b
, b 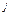 – невід’ємні: а
– невід’ємні: а 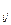 , b
, b 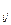 ≥ 0, i = 1,…,n, j = 1, 2,…, m.
≥ 0, i = 1,…,n, j = 1, 2,…, m.
Введемо до розгляду прямокутні матриці А = (а 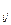 ), В = (b
), В = (b 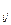 ), А ≥ 0, В ≥ 0. Вектори a
), А ≥ 0, В ≥ 0. Вектори a 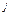 та b
та b 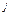 є стовпцями матриць А та В відповідно.
є стовпцями матриць А та В відповідно.
Кажуть, що технологію моделі задає пара невід’ємних матриць (А, В). Матрицю А називають матрицею витрат, а матрицю В – матрицею випуску.
На підставі базисних процесів побудуємо новий процес, в котрому витрати і випуск є лінійною комбінацією відповідних векторів a 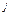 , b
, b 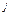 :
:
 = (Ах, Вх) (1)
= (Ах, Вх) (1)
де вектор х = (х  , х
, х 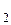
 , …, х
, …, х  ), х
), х  ≥ 0, j = 1, 2, …, m називається вектором інтенсивностей. Будемо при цьому говорити, що j –й базисний процес (a
≥ 0, j = 1, 2, …, m називається вектором інтенсивностей. Будемо при цьому говорити, що j –й базисний процес (a 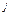 , b
, b 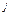 ) приймає участь в процесі (Ах, Вх) з інтенсивністю х
) приймає участь в процесі (Ах, Вх) з інтенсивністю х 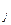 . Літерою С позначимо множину процесів
. Літерою С позначимо множину процесів
С = 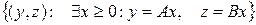 (2)
(2)
Модель Леонтьєва є частковим випадком моделі Неймана при n = m, В =І.
Опишемо динаміку моделі фон Неймана.
Припущення1. Модель Неймана лінійна
Через х  будемо позначати вектор інтенсивностей, який описує функціонування моделей на проміжку [ t-1, t ]. Будемо розглядати Т періодів часу. В кожен із таких періодів [ t-1, t ] для виробництва продукції застосовується один із процесів множини С, він характеризується певним вибором вектора інтенсивностей xt.
будемо позначати вектор інтенсивностей, який описує функціонування моделей на проміжку [ t-1, t ]. Будемо розглядати Т періодів часу. В кожен із таких періодів [ t-1, t ] для виробництва продукції застосовується один із процесів множини С, він характеризується певним вибором вектора інтенсивностей xt.

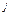 , b
, b 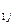 , а
, а  ,…, а
,…, а  ) описує витрати, а n -вимірний вектор b
) описує витрати, а n -вимірний вектор b 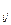 , b
, b  = (Ах, Вх) (1)
= (Ах, Вх) (1) , х
, х 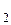
 , …, х
, …, х  ), х
), х  ≥ 0, j = 1, 2, …, m називається вектором інтенсивностей. Будемо при цьому говорити, що j –й базисний процес (a
≥ 0, j = 1, 2, …, m називається вектором інтенсивностей. Будемо при цьому говорити, що j –й базисний процес (a 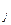 . Літерою С позначимо множину процесів
. Літерою С позначимо множину процесів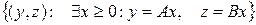 (2)
(2) будемо позначати вектор інтенсивностей, який описує функціонування моделей на проміжку [ t-1, t ]. Будемо розглядати Т періодів часу. В кожен із таких періодів [ t-1, t ] для виробництва продукції застосовується один із процесів множини С, він характеризується певним вибором вектора інтенсивностей xt.
будемо позначати вектор інтенсивностей, який описує функціонування моделей на проміжку [ t-1, t ]. Будемо розглядати Т періодів часу. В кожен із таких періодів [ t-1, t ] для виробництва продукції застосовується один із процесів множини С, він характеризується певним вибором вектора інтенсивностей xt.


