Коб запропонував функцію виду
 (1)
(1)
де Y - обсяг виробленої продукції;
 – капіталовкладення
– капіталовкладення
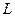 – трудові ресурси
– трудові ресурси
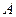 ,
,  ,
,  - числові параметри
- числові параметри
 ,
, 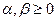 ,
, 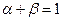
Було складено систему рівнянь
 ,
, 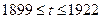
де 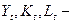 фактичні значения відповідних величин в рік
фактичні значения відповідних величин в рік  . Методом найменших квадратів було знайдено значення параметрів
. Методом найменших квадратів було знайдено значення параметрів 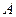 ,
,  ,
,  , які відповідно мінімізували вираз
, які відповідно мінімізували вираз
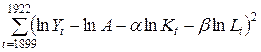
При цьому з’ясувалось, що  ,
,  ,
, 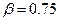 ;
;
Тобто було встановлено, що  .
.
Перевірка адекватності моделі 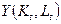 з фактичними даними засвідчила, що отримана залежність дає дуже хороше наближення, а найбільші відхилення величин
з фактичними даними засвідчила, що отримана залежність дає дуже хороше наближення, а найбільші відхилення величин 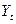 і
і 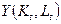 спостерігались тільки в періоди економічної депресії або надмірного оживлення ділової активності.
спостерігались тільки в періоди економічної депресії або надмірного оживлення ділової активності.
В науковому плані це був чудовий старт і зараз теорія виробничих функцій дуже широко застосовується для задач планування і прогнозування як в окремих галузях, так і на рівні всього народного господарства.
Для вивчення основних математичних характеристик виробничих функцій і їх економічної інтерпретації розглянемо двох факторну функцію
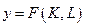 (2)
(2)
де 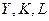 - мають той самий смисл, що і в функції Коба-Дугласа (1). Функцію (1) ми будемо і надалі використовувати в якості практичної ілюстрації.
- мають той самий смисл, що і в функції Коба-Дугласа (1). Функцію (1) ми будемо і надалі використовувати в якості практичної ілюстрації.
На виробничу функцію (2) накладаються наступні умови:
1) 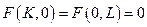 ; (3)
; (3)
2)  ,
, 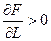 ; (4)
; (4)
3)  ,
, 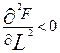 ; (5)
; (5)
4)  ,
, 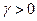 ,
,  (6)
(6)
Коротко пояснимо накладені вимоги:
(3) – при відсутності одного з факторів виробництва, випуск продукції неможливий;
(4) – при збільшенні об’єму одного з факторів, якщо інший – незмінний, випуск продукції зростає;
(5) – якщо один з факторів зафіксувати, то збільшення приросту другого фактора призводить до зменшення темпів приросту випуску продукції;
(6) – умова однорідності степені 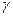 . Показник
. Показник 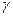 характеризує ефект від розширення масштабу виробництва. Якщо
характеризує ефект від розширення масштабу виробництва. Якщо 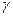 >1, то одночасне збільшення всіх факторів в
>1, то одночасне збільшення всіх факторів в  разів, призводить до зростання об’єму випуску більше ніж в
разів, призводить до зростання об’єму випуску більше ніж в  разів.
разів.
На практиці найчастіше  .
.
Розглянемо основні економіко-математичні характеристики виробничих функцій:
 - середня (питома) продуктивність праці; (7)
- середня (питома) продуктивність праці; (7)
 - середня (питома) фондовіддача; (8)
- середня (питома) фондовіддача; (8)
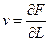 - гранична продуктивність праці; (9)
- гранична продуктивність праці; (9)
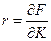 - гранична фондовіддача; (10)
- гранична фондовіддача; (10)
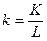 - фондоозброєність (кількість капіталовкладень на одного працівника).
- фондоозброєність (кількість капіталовкладень на одного працівника).
Всі перераховані показники є розмірними величинами, зв’язаними з абсолютними приростами. Представляють інтерес величини, які характеризують процент приросту продукції при збільшенні затрат ресурсу на 1%. Такі показники називаються коефіцієнтами еластичності.
Коефіцієнт еластичності по фондах:
 (11)
(11)
Пояснимо цю формулу. Нехай приріст 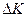 основних фондів при незмінному другому факторі - трудових ресурсів, відповідає приросту
основних фондів при незмінному другому факторі - трудових ресурсів, відповідає приросту 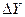 об’єму випуску. Тоді збільшення об’єму основних фондів
об’єму випуску. Тоді збільшення об’єму основних фондів 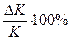 відповідає збільшенню випуску на
відповідає збільшенню випуску на 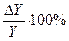 . Отже, при збільшенні об’єму основних фондів на 1%, об’єм випуску збільшиться на
. Отже, при збільшенні об’єму основних фондів на 1%, об’єм випуску збільшиться на  .. Переходячи до границі при
.. Переходячи до границі при 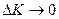 , отримаємо формулу (11).
, отримаємо формулу (11).
Коефіцієнт еластичності по праці
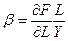 (12)
(12)
має аналогічний зміст.
Покажемо, що (1) задовольняє умовам виробничих функцій (3) – (6) і визначимо відповідні характеристики для функції Коба-Дугласа.
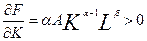 ;
;
 ;
;
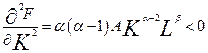 , бо
, бо  ;
;
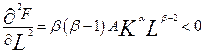
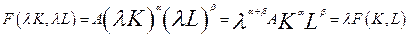
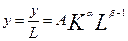 ,
, 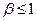
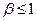 , тому середня продуктивність праці функції Коба-Дугласа є спадною за аргументом
, тому середня продуктивність праці функції Коба-Дугласа є спадною за аргументом 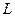 . Тобто зі збільшенням затрат середня продуктивність праці падає. Пояснення: оскільки величина другого фактора К незмінна, то додатково залучена робоча сила не забезпечена додатковими засобами виробництва, що і призводить до зниження продуктивності праці.
. Тобто зі збільшенням затрат середня продуктивність праці падає. Пояснення: оскільки величина другого фактора К незмінна, то додатково залучена робоча сила не забезпечена додатковими засобами виробництва, що і призводить до зниження продуктивності праці.
Аналогічно
 ,
, 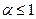
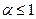 , тому середня продуктивність праці є спадною;
, тому середня продуктивність праці є спадною;
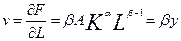 , тобто гранична продуктивність праці пропорційна середній продуктивності і завжди менша за неї, бо
, тобто гранична продуктивність праці пропорційна середній продуктивності і завжди менша за неї, бо  , тому
, тому 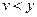 .
.
Аналогічно
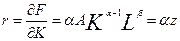
Коефіцієнт еластичності по фондах (капіталовкладення)
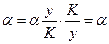 , тобто власне параметр
, тобто власне параметр  у функції Коба-Дугласа і є коефіцієнтом еластичності по фондах, а
у функції Коба-Дугласа і є коефіцієнтом еластичності по фондах, а  є коефіцієнтом еластичності по праці. Ці коефіцієнти для функції Коба-Дугласа не залежать від величин факторів К та
є коефіцієнтом еластичності по праці. Ці коефіцієнти для функції Коба-Дугласа не залежать від величин факторів К та 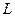 .
.

 (1)
(1) – капіталовкладення
– капіталовкладення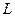 – трудові ресурси
– трудові ресурси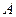 ,
,  ,
,  - числові параметри
- числові параметри ,
, 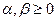 ,
, 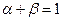
 ,
, 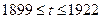
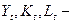 фактичні значения відповідних величин в рік
фактичні значения відповідних величин в рік  . Методом найменших квадратів було знайдено значення параметрів
. Методом найменших квадратів було знайдено значення параметрів 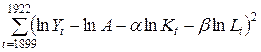
 ,
,  ,
, 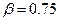 ;
; .
.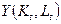 з фактичними даними засвідчила, що отримана залежність дає дуже хороше наближення, а найбільші відхилення величин
з фактичними даними засвідчила, що отримана залежність дає дуже хороше наближення, а найбільші відхилення величин 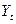 і
і 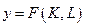 (2)
(2)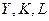 - мають той самий смисл, що і в функції Коба-Дугласа (1). Функцію (1) ми будемо і надалі використовувати в якості практичної ілюстрації.
- мають той самий смисл, що і в функції Коба-Дугласа (1). Функцію (1) ми будемо і надалі використовувати в якості практичної ілюстрації.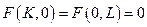 ; (3)
; (3) ,
, 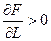 ; (4)
; (4) ,
, 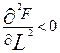 ; (5)
; (5) ,
, 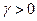 ,
,  (6)
(6)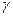 . Показник
. Показник  разів, призводить до зростання об’єму випуску більше ніж в
разів, призводить до зростання об’єму випуску більше ніж в  .
. - середня (питома) продуктивність праці; (7)
- середня (питома) продуктивність праці; (7) - середня (питома) фондовіддача; (8)
- середня (питома) фондовіддача; (8)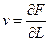 - гранична продуктивність праці; (9)
- гранична продуктивність праці; (9)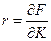 - гранична фондовіддача; (10)
- гранична фондовіддача; (10)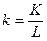 - фондоозброєність (кількість капіталовкладень на одного працівника).
- фондоозброєність (кількість капіталовкладень на одного працівника). (11)
(11)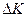 основних фондів при незмінному другому факторі - трудових ресурсів, відповідає приросту
основних фондів при незмінному другому факторі - трудових ресурсів, відповідає приросту 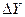 об’єму випуску. Тоді збільшення об’єму основних фондів
об’єму випуску. Тоді збільшення об’єму основних фондів 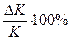 відповідає збільшенню випуску на
відповідає збільшенню випуску на 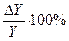 . Отже, при збільшенні об’єму основних фондів на 1%, об’єм випуску збільшиться на
. Отже, при збільшенні об’єму основних фондів на 1%, об’єм випуску збільшиться на  .. Переходячи до границі при
.. Переходячи до границі при 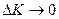 , отримаємо формулу (11).
, отримаємо формулу (11).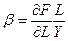 (12)
(12)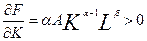 ;
; ;
;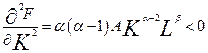 , бо
, бо  ;
;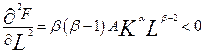
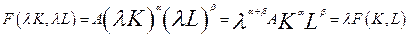
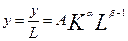 ,
, 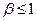
 ,
, 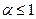
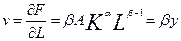 , тобто гранична продуктивність праці пропорційна середній продуктивності і завжди менша за неї, бо
, тобто гранична продуктивність праці пропорційна середній продуктивності і завжди менша за неї, бо  , тому
, тому 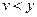 .
.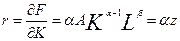
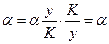 , тобто власне параметр
, тобто власне параметр  є коефіцієнтом еластичності по праці. Ці коефіцієнти для функції Коба-Дугласа не залежать від величин факторів К та
є коефіцієнтом еластичності по праці. Ці коефіцієнти для функції Коба-Дугласа не залежать від величин факторів К та 


