Примітивні матриці. Стійкість
При вивченні властивостей моделі Леонтьєва, а також її динамічного аналога, поняття Фробеніусових числа і вектора мають фундаментальне значення. В динамічній моделі також істотною є інформація про асимптотичну поведінку послідовності матриць Ak. Введемо в Rn норму за таким правилом:
При цьому pA (власний вектор двоїстої задачі) вибираємо так, що (pA, pА) = 1. Означення: Нехай матриця A нерозкладна і Приклад Матриця A = Невід’ємні матриці ми розбили на 2 класи, які між собою не перетинаються – нерозкладні та розкладні матриці. Нерозкладні матриці в свою чергу теж поділяються на 2 несумісні класи – циклічні матриці та примітивні. Означення. Нерозкладна матриця А називається циклічною (або імпримітивною), якщо множину Приклад. Матриця
|

 || x ||A = (| x |, pA)
|| x ||A = (| x |, pA) x послідовність векторів {
x послідовність векторів { 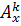 }, k =1,2,… збігається. Тоді матриця A називається стійкою.
}, k =1,2,… збігається. Тоді матриця A називається стійкою.
 не є стійкою. Якщо вектор x = (x1,x2), де x1≠ x2, то послідовність {
не є стійкою. Якщо вектор x = (x1,x2), де x1≠ x2, то послідовність { 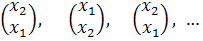 ,
,  і не є збіжною. Звичайно, при x1 = x2 виписана послідовність збігається, бо є стаціонарною, але в означенні стійкої матриці збіжність повинна мати місце для довільного вектора x.
і не є збіжною. Звичайно, при x1 = x2 виписана послідовність збігається, бо є стаціонарною, але в означенні стійкої матриці збіжність повинна мати місце для довільного вектора x. можна представити у вигляді
можна представити у вигляді 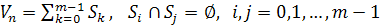 , причому, якщо
, причому, якщо  , то
, то 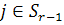 , а при
, а при 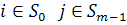 .
. є циклічною. Справді,
є циклічною. Справді,  .
.


