Означення 2. Нехай S - підмножина з . Якщо при , то множину S будемо називати ізольованою.
Приклад
Економічна інтерпретація введеного поняття у випадку моделі Лєонтєва очевидна: якщо S ізольована множина, то галузі з множини S не використовують у виробничому процесі продукцію галузей, номери яких належить S’, тобто група галузей з номерами з S може функціонувати незалежно від інших галузей. У випадку моделі обміну ізольованість множини S означає, що країни з номерами з S не імпортують товарів з країни з номерами Перенумеруємо індекси так, щоб S= {1,2,…,k}. В матриці А це означає одночасну перестановку рядків і стовпчиків, після чого матриця А записується у вигляді:
де Так, якщо в матриці А з прикладу виконати перестановку 1 і 3 стовпців, а потім 1 і 3 рядків, то будемо мати
k=1, n-k=2 і тепер S={1} і Матрицю С жодними перестановками рядків і стовпців до виду (1) звести не можна. Означення 3. Якщо для деякої матриці А розміру n*n у множині Нерозкладну матрицю А одночасними перестановками стовпців і рядків не можна звести до виду (1). Матриця А>0 будь-якого розміру нерозкладна. Якщо в матриці розміру n>=3 лише один елемент рівний 0, то така матриця нерозкладна.
Економічне тлумачення поняття нерозкладності матриці. Для моделі Леонтьєва кожна з галузей використовує принаймні непрямо продукцію всіх галузей з даної системи. Так у випадку матриці С третя галузь продукцію другої галузі використовує безпосередньо, (бо
|

 S={3}
S={3} 
 - ізольованих множин не має.
- ізольованих множин не має.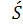 , при цьому експорт, взагалі кажучи, можливий.
, при цьому експорт, взагалі кажучи, можливий. (1)
(1)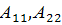 - квадратні блоки розмірів k*k і (n-k)*(n-k) відповідно.
- квадратні блоки розмірів k*k і (n-k)*(n-k) відповідно.
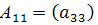
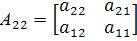
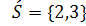
 немає ізольованих підмножин, то таку матрицю будемо називати нерозкладною.
немає ізольованих підмножин, то таку матрицю будемо називати нерозкладною.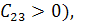 але для виготовлення продукції другої галузі використовуються надходження з 1-ої і 3-ої:
але для виготовлення продукції другої галузі використовуються надходження з 1-ої і 3-ої:  .
.


