Властивості нерозкладних матриць.
1. Якщо матриця А нерозкладна, що вона не може мати ні нульових рядків ні нульових стовпчиків. ▼ Справді, якщо j стовпчик нульовий, то S={j} ізольована множина. Якщо нульовий і -ий рядок, то S= ▲ 2. Якщо матриця А нерозкладна, а вектор
▼Властивість очевидна, оскільки матриця не має нульових рядків. ▲ 3. Нехай А - нерозкладна матриця, вектор y
▼Доведення. Від супротивного. Якщо позначити
▲ 4. Нехай у - невід’ємний ненульовий вектор ( ▼Доведення. Перш за все, оскільки Від супротивного. Припустимо, що серед координат вектора x є нульові, тобто множина ▲ 5. Якщо А - нерозкладна матриця розмірності n*n, то ▼Доведення. Дійсно за властивістю 4)
▲ 6. Якщо А - нерозкладна, то для будь-якої пари індексів (i,j),
▼Справді, запишемо розклад за формулою бінома Ньютона.
Нехай спочатку 7. Для того, щоб матриця А була нерозкладною, необхідно і достатньо, щоб для будь-яких індексів i,j існувала послідовність 8. Якщо матриця А нерозкладна, а
|

 ізольована підмножина.
ізольована підмножина.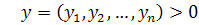 , то вектор
, то вектор 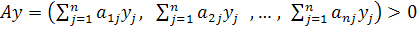
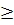 0, а
0, а 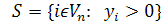 і нехай z=Ay, T
і нехай z=Ay, T  . Якщо при цьому
. Якщо при цьому  і
і 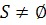 , то
, то
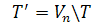 і припустити
і припустити 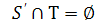 , то
, то  , а
, а  . Візьмемо
. Візьмемо 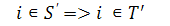 і тому
і тому 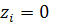 і
і . Оскільки
. Оскільки  , то це можливо лише тоді, коли
, то це можливо лише тоді, коли  . Отже S - ізольована, що суперечить, що А - нерозкладна.
. Отже S - ізольована, що суперечить, що А - нерозкладна.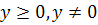 ), а вектор z=(I+A)y. Позначимо через
), а вектор z=(I+A)y. Позначимо через 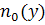 число координат вектора у,
число координат вектора у,  . Тоді
. Тоді  при
при  і
і 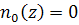 при
при  . Крім цього, якщо А - нерозкладна,
. Крім цього, якщо А - нерозкладна, 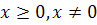 , то у нерівності
, то у нерівності  будемо мати
будемо мати  .
.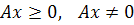 , то
, то 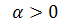 .
.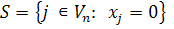 непорожня. За властивістю 3) знайдеться
непорожня. За властивістю 3) знайдеться  такий що,
такий що,  , але тоді неможлива нерівність
, але тоді неможлива нерівність  .
. , тобто всі елементи матриці
, тобто всі елементи матриці 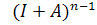 є строго додатніми.
є строго додатніми.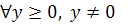 маємо, що
маємо, що
 знайдеться натуральне число m таке, що
знайдеться натуральне число m таке, що 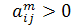 (через
(через 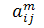 позначено відповідний елемент матриці
позначено відповідний елемент матриці 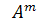 ).
). (2)
(2) . Серед чисел
. Серед чисел  обов’язково є додатне: в протилежному випадку, як впливає з формули (2), (i,j) -ий елемент матриці
обов’язково є додатне: в протилежному випадку, як впливає з формули (2), (i,j) -ий елемент матриці  , яка за властивостями 2) і 6) є додатною
, яка за властивостями 2) і 6) є додатною 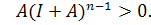
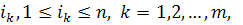 така що
така що  ,
, 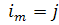 ,
, 
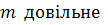 число з
число з  , то в матриці
, то в матриці  не можна бути ні нульових рядків, ні нульових стовпчиків.
не можна бути ні нульових рядків, ні нульових стовпчиків.


