Расчет стоимости капитала
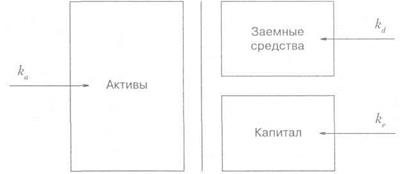
Стоимость капитала вытекает из базового линейного соотношения между риском и доходностью, которое мы только что рассмотрели. Мы можем посмотреть на него с двух сторон, в зависимости от того, на какой стороне баланса мы сделаем акцент.
Стоимость долга kd равна rf + βd * (rm-rf)
2 Cm. «Wall Street and the amazing vanishing risk premium», Financial Times, 22 Это ожидаемая ставка доходности, которую требуют инвесторы, предоставляющие фирме заемные средства. Стоимость акционерного капитала ke равна rf + βe * (rm-rf) Это ожидаемая ставка доходности держателей акционерного капитала для того, чтобы компенсировать стоимость упущенных возможностей и риски. Рентабельность активов ka равна rf + βa * (rm-rf) Это ожидаемая норма прибыли, которую должна получать компания для того, чтобы удовлетворить требования всех инвесторов (предоставляющих как заемный, так и собственный капитал). Если мы обозначим за D рыночную стоимость заемных средств, за Е — рыночную стоимость акционерного капитала и за V — суммарную рыночную стоимость фирмы, очевидно, мы должны получить следующее соотношение: ka = D/V*kd + E/V*ke. (1) Учитывая то, что rf и (rm-rf) одинаковы для этих трех стоимостей, мы можем прийти к следующей формуле: βa = D/V* βd + E/V*βe. (2) Другими словами, β; активов является средневзвешенной величиной β; обязательств и β; собственного капитала. На практике, считая, что βd довольно мала, мы пренебрегаем ею, и это позволяет нам упростить уравнение (2) следующим образом: βa = E/V*βe (3) Отметим, что бетой активов βa иногда называют бету фирмы, не использующей рычага (левериджа) (unlevered). Ее иногда обозначают в расчетах βu. Коэффициентом β; акционерного капитала (βe), соответственно, называют бету фирмы, использующей рычаг (levered) и обозначают как βl Вообще, расчет беты требует учета соотношения между рыночной стоимостью акционерного капитала и стоимостью фирмы1. Когда у компании нет заемных средств, т. е. она не подвержена воздействию рычага, бета активов, очевидно, равна бете собственного
  U = означает отсутствие рычага (unlevered) L = означает наличие рычага (levered) A = активы U = означает отсутствие рычага (unlevered) L = означает наличие рычага (levered) A = активыЕ = акционерный капитал D = заемный каптал Вu=ВА BL=BE
Ba=(E/V)BeoBu = (E/V)Bl Ки = RF + Ви (RM + RF) о Кд =RF + BA (RM + RF)
капитала. Вся эта терминология и математические соотношения сведены воедино на рис. 4.4. Проиллюстрируем все эти соотношения на простом примере. Компания X имеет следующий баланс (в миллионах €) по рыночной стоимости:
Rf равна 5%, и рыночная премия по акционерному капиталу считается равной 6%. Компания X имеет β; акционерного капитала 1,3 и берет деньги в долг по ставке rf, (это означает, что ее заемный капитал не подвержен риску и (βd = 0). Тогда стоимость акционерного капитала &е равна 5% + 1,3x6% = 12,8%. «Смешанная» стоимость капитала': D/Vxkd + E/Vxke, следовательно, будет равняться 40% х 5% + 60% х 12,8% = 9,68%. Исключая воздействие рычага на b акционерного капитала и применяя уравнение (3), мы можем найти b активов: β; а= E/V х βe => 60% х 1,3 = 0,78. Рентабельность активов ka равна К а= r/+ ba x (rm - rf) = 5% + 0,78 (6%) = 9,68%. 4.2.1. Метод средневзвешенной стоимости капитала (WACCj: анализ правой стороны баланса WACC2 определяется как ставка, требуемая как кредиторами, так и акционерами фирмы (см. уравнение (1)), с учетом налоговых вычетов по процентам. Если компания является рентабельной и налоговая ставка равна t, то стоимость заемных средств после налогообложения kdAT будет равна k/jt умноженное на (1 — t). Следовательно, WACC выражается следующей формулой: WACC = D/Vxkdx(l-t) + E/Vxke. (4) Необходимо помнить, что kdnke— это числа, связанные с конкретной структурой капитала. Это означает, что kd и ke являются функциями соотношения заемного и собственного капитала. Поэтому, какая бы структура капитала ни применялась, необходимо использовать kd и ke, согласованные со структурой капитала. При расчете WACC фирм мы будем использовать целевую структуру капитала, т. е. такую структуру капитала, измеренную по рыночной стоимости, которую компания намерена получить или обязана поддерживать на протяжении некоторого времени. Следовательно, в уравнении (4): ♦ D/V — это процент заемных средств в целевой структуре капита ♦ E/V— это процент акционерного капитала в целевой структуре капи
2 WACC— Weighted Average Cost of Capital. — Прим. перев. ♦   kd— доходность, требуемая кредиторами фирмы (заимодавцами, kd— доходность, требуемая кредиторами фирмы (заимодавцами,держателями облигаций); ♦ ke — ожидаемая доходность, требуемая акционерами; ♦ t — ставка налога на прибыль1. Ниже рассчитана WAСС для примера из предыдущего раздела при маржинальной налоговой ставке 40%: WACC = 40% х 5% [0,6] + 60% х 12,8% = 8,88%. Разница между величинами 8,88 и 9,68%, полученными нами ранее для ка, показывает влияние налогового вычета, связанного с процентами, выплаченными по заемным средствам. Оценка kd обычно не составляет проблемы. Это ставка, явно оговоренная в контракте, и потому ее обычно бывает довольно просто оценить. В то же время мы должны заметить, что такую доходность данная компания обещает заплатить по своим долгам, что не совсем совпадает с доходностью, которую ожидают получить держатели долговых обязательств. Используя эту обещанную доходность в качестве заменителя ожидаемой доходности, мы подразумеваем, что вероятность невыполнения данной компанией своих обязательств довольно низкая (что является обоснованным предположением, если компания имеет инвестиционный кредитный рейтинг). Чтобы оценить доходность, ожидаемую акционерами, мы применяем модель оценки доходности финансовых активов: k e = rf + βe * (rm-rf) Это легко сделать при условии, что акции этой компании продаются на рынке ценных бумаг, и мы можем рассчитать или получить значение (3. Если мы рассматриваем частную компанию, структурную единицу или часть холдинговой компании, нам приходится полагаться на данные сопоставимых фирм, для которых мы можем получить оценки коэффициентов бета. Эти коэффициенты отражают основной деловой риск и финансовый риск. Если мы выбрали наши сопоставимые компании из той же отрасли, что и предприятие, которое мы хотим оценить, то можно
предположить, что их риск будет близким. Но что если финансовый риск, т. е. структура заемных средств, различается? Тогда мы должны сначала устранить воздействие левериджа на β; нашего сопоставимого предприятия, чтобы получить β; активов, а затем вновь учесть его, используя данные о целевой структуре капитала нашей компании. Продемонстрируем эту методику на простом примере. Предположим, что вы размышляете о приобретении частной компании, которая имеет 20% заемных средств в общей сумме капитала. Существует похожая компания, занимающаяся таким же бизнесом и, следовательно, подверженная таким же рискам, с бета 1,8 и коэффициентом заемных средств 50%'. Безрисковая норма прибыли равна 5%, а премия за риск на рынке акционерного капитала — 6%. Вас интересует, какую стоимость акционерного капитала следует применить при оценке WACC, чтобы произвести оценку данной компании? Первый шаг — это устранить воздействие рычага на коэффициент бета сопоставимой компании, используя уравнение (3): βa = E/V*βe Если D/V равно 0,5 (50%), то Е/V тоже равно 0,5. => βa = 1,8x0,5 = 0,9. Это означает, что компании, финансирующие свою деятельность только за счет собственных средств, в этом виде бизнеса имеют 3 = 0,9. Вторым шагом является приложение рычага к полученному 3 с использованием структуры капитала нашей целевой компании. Уравнение (3) может быть записано как: βe = E/V*βa
Применяя уравнение (4), мы получим 3 акционерного капитала нашей компании следующим образом: V/E- 1,25 (если D/V- 0,2 =>E/V= 0,8 =>V/E- 1/0,8 =1,25); βe =0,9x1,25 -1,13. Третий шаг — рассчитать стоимость акционерного капитала (ke) рассматриваемой компании, используя коэффициент бета акционерного капитала 1,13: ke =5%+1,13x6% = 11,78%.
  Если мы вложим деньги в акционерный капитал этой компании, нам следует ожидать доходности наших инвестиций, близкой к 11,8%. Если мы вложим деньги в акционерный капитал этой компании, нам следует ожидать доходности наших инвестиций, близкой к 11,8%.
Мы использовали упрощенную формулу для устранения действия рычага (уравнения (3) и (4)), что предполагает, что заемные активы являются безрисковыми (βd = 0) и что величина заемных средств пропорциональна общей стоимости фирмы. Иначе говоря, мы предполагали, что рассматриваемая фирма меняет сумму заемных средств пропорционально изменению общей стоимости фирмы1. Рисунок 4.5 обобщает различные элементы WACC. Чтобы применять WACC, не забывайте о следующих моментах: ♦ Предполагайте постоянство структуры капитала, что означает, ♦ Стоимость заемных средств (kd) и стоимость акционерного капи ♦ При измерении D/Vu E/V используйте рыночные веса. ♦ Считайте, что рассматриваемая фирма действительно имеет це ♦ Налоговая ставка постоянна, и данная фирма может использовать
βe = (E + D(l - t))/E х βa, где t — это ставка налога. Если заемные средства не являются безрисковыми (βd > 0), формула становится более сложной. 2 Понятно, что существуют категории компаний, для которых это неспра 
Рис. 4.5. Оценка элементов WACC Нам не следует забывать, что если мы отходим от этих предположений, становится рискованным использовать WACC, а модификации моделей, которые следует делать, будут, вероятно, очень сложными. 4.2.2. Стоимость капитала с точки зрения активов, или стоимость капитала, не подверженного воздействию рычага: анализ левой стороны баланса Поскольку мы оцениваем активы, почему бы нам не дисконтировать потоки денежных средств, ожидаемые от активов, по стоимости капитала, не подверженного воздействию рычага, и не рассчитать налоговую защиту как отдельный компонент? Это основа метода APV (метода откорректированной текущей стоимости), описанного в следующей главе. Если коэффициенты бета для активов известны, этот метод был бы существенным шагом вперед, поскольку нам не надо было бы думать о структуре капитала фирмы и мы могли бы сконцентрироваться только на левой стороне баланса, т. е. на стороне активов. К сожалению, мы редко наблюдаем коэффициенты бета для активов, поскольку активы и потоки денежных средств, связанные с ними, редко продаются на

|

 1 Эти коэффициенты можно найти для американских компаний США через
1 Эти коэффициенты можно найти для американских компаний США через BA=(E/V) BE=(D/V) BE«Bu=(D/V) BD=(D/V) BL
BA=(E/V) BE=(D/V) BE«Bu=(D/V) BD=(D/V) BL Ки = D/V KD + E/V КЕ, что подобно WACCA без налоговой защиты
Ки = D/V KD + E/V КЕ, что подобно WACCA без налоговой защиты Рис. 4.4. Терминология и математические соотношения
Рис. 4.4. Терминология и математические соотношения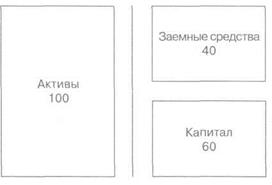
 1 Мы используем термин «смешанная» стоимость капитала, чтобы отличить ее от средневзвешенной стоимости капитала, которая, как показано в следующем разделе, принимает во внимание налоги.
1 Мы используем термин «смешанная» стоимость капитала, чтобы отличить ее от средневзвешенной стоимости капитала, которая, как показано в следующем разделе, принимает во внимание налоги. 1 Ричард С. Рубак (Richard S. Ruback) показал в различных документах, в част
1 Ричард С. Рубак (Richard S. Ruback) показал в различных документах, в част 1 APV — Adjusted Present Value. — Прим. перев.
1 APV — Adjusted Present Value. — Прим. перев.
 рынке в такой форме, которую можно было бы отслеживать, в то время как акционерный капитал продается на финансовом рынке в виде ценных бумаг, и поэтому мы способны вычислять для него коэффициенты бета. Уравнение (3), использующее коэффициенты бета акционерного капитала после устранения действия рычага, позволяет нам получить коэффициенты бета для активов (или, как мы их иногда называем, коэффициенты бета, не подверженные воздействию рычага). Таблица 4.5 показывает взаимосвязь между WA СС и ka (рентабельность активов, не зависящих от воздействия), что дает упрощенный метод расчета WACC u, следовательно, полезный способ приблизиться к нему.
рынке в такой форме, которую можно было бы отслеживать, в то время как акционерный капитал продается на финансовом рынке в виде ценных бумаг, и поэтому мы способны вычислять для него коэффициенты бета. Уравнение (3), использующее коэффициенты бета акционерного капитала после устранения действия рычага, позволяет нам получить коэффициенты бета для активов (или, как мы их иногда называем, коэффициенты бета, не подверженные воздействию рычага). Таблица 4.5 показывает взаимосвязь между WA СС и ka (рентабельность активов, не зависящих от воздействия), что дает упрощенный метод расчета WACC u, следовательно, полезный способ приблизиться к нему.


