Температура

Температура системы, находящейся в равновесном состоянии, является мерой интенсивности теплового движения молекул, образующих систему. В этом состоит молекулярно-кинетическое истолкование температуры.

Если соприкасающиеся тела находятся в состоянии теплового равновесия, т.е., не обмениваются энергией путем теплопередачи, то им приписывают одинаковую температуру, а если при тепловом контакте одно из них передает энергию другому посредством теплопередачи, то первому приписывают большую температуру, второму – меньшую.

Средняя кинетическая энергия теплового движения частиц прямо- пропорциональна термодинамической температуре системы.

Для измерения температуры используется зависимость от температуры ряда физических свойств тела, называемого термометрическим, при прямом или косвенном измерении: длина, объем, сопротивление и др. Их изменение является основой для измерения температуры.

Для практического измерения температуры применяются температурные шкалы, установленные с помощью термометрических тел. В Международной стоградусной шкале в качестве термометрического тела берется вода и температура выражается в градусах Цельсия. В термодинамической температурной шкале температура выражается в К и называется термодинамической температурой. Связь между шкалами . К называется абсолютный нуль температуры или нуль по термодинамической шкале.

 

1.4 Уравнение состояния идеального газа

Состояние данной массы газа определяется значением трех параметров , изменение одного из них приводит к изменению других. Соотношение, связывающее эти параметры, представляет собой уравнение состояния данной массы газа.

Простейшим объектом, для которого рассмотрено уравнение состояния, является идеальный газ. Это газ, взаимодействием между молекулами которого можно пренебречь. Всякий реальный газ при достаточном разрежении близок к идеальному при комнатной температуре, особенно гелий и водород.

Экспериментально показано, что при небольших плотностях газы с хорошей точностью подчиняются уравнению:

(1) - уравнение состояния идеального газа.

Согласно закону Авогадро 1 моль любого газа занимает при одинаковых условиях ( и ) одинаковый объем. В частности, при нормальных: 1 атм. и 273К объем одного моля газа равен 22,4 л. Значит, в формуле (1) для 1 моля любого газа величина константы будет одной и той же. Она обозначается как - универсальная газовая постоянная, = 8,31Дж/моль К. Тогда уравнение состояния 1 моля газа: (2).

Теперь можно записать уравнение для произвольной массы газа, учитывая, что при одинаковых и число молей газа будет занимать объем в раз больше: , тогда умножив (2) на , получим: (3) – уравнение состояния для произвольной массы газа. Оно называется также уравнением Менделеева – Клапейрона.

Если его правую часть умножить и разделить на число Авогадро, то получим:

. Или учитывая, что - постоянная Больцмана, а 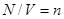- концентрация, получим окончательно:

-еще одна форма уравнения состояния идеального газа.