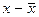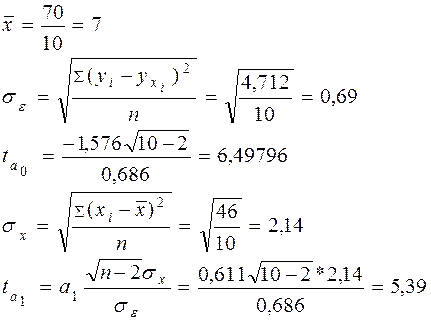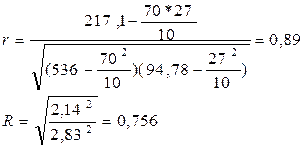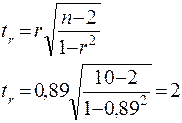Применение корреляционно-регрессивного анализа связи
Рассмотрим влияние вариации факторного показателя х на результативный у. Пример. Имеется следующая информация по однотипным предприятиям о возрасте (продолжительности эксплуатации) силового оборудования и затратах на его ремонт.
В условиях использования ЭВМ выбор адекватной математической функции осуществляется перебором решений наиболее часто применяемых. Наиболее часто встречается прямолинейная зависимость. ух=а0+а1х Для определения параметров уравнения
Расчетная таблица.
а0=(27*536-217,1*70)/(10*536-70*70)=-1,576 а1=(10*217,1-70*27)/460=0,611 Зависимость расходов на ремонт от возраста оборудования. ух=-1,576+0,611х Проверим эту формулу на типичность:
Для определения ух1=-1,576+0,611*4=0,868 ух2,3=-1,576+0,611*5=1,479 ух4,10=-1,576+0,611*6=2,09 ух5,7=-1,576+0,611*8=3,312 ух6=-1,576+0,611*10=4,534 ух8=-1,576+0,611*7=2,701 ух9=-1,576+0,611*11=5,145
Расчетная таблица
В экономико-статистических исследованиях принято, что уровень значимости а=0,05 и число степеней свободы k=10-2, то табличное критическое значение tk= 5,32. Сравнение фактических и табличных значений t-критерия ta0>tk<ta1 Это позволяет признать вычисленные по уравнению параметры типичными.
Полученная величина R=0,756 означает, что в соответствии со шкалой Чеддока установленная по уравнению регрессии связь между затратами на ремонт и возрастом оборудования высокая. Оценка значимости коэффициента корреляции осуществляется по t-критерию. Фактическое значение этого критерия
При критическом значении tk=2,3 получается, что tr>tk. Вычисленный коэффициент корреляции признается существенным.
|

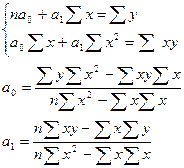
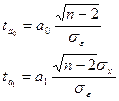
 на основе формулы определяем выравненные значения ухi
на основе формулы определяем выравненные значения ухi